Théorie¶
1. Implication¶
Considérons plusieurs propositions relevant respectivement d’un contexte géométrique, arithmétique et de la vie courante.
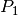 : Les diagonales du quadrilatère
: Les diagonales du quadrilatère 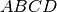 se
coupent en leur milieu.
se
coupent en leur milieu. : Le quadrilatère
: Le quadrilatère 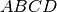 est un parallélogramme.
est un parallélogramme.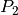 :
:  est un naturel multiple de 4.
est un naturel multiple de 4. :
:  est un naturel multiple de 2.
est un naturel multiple de 2.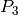 : Il pleut.
: Il pleut.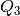 : Ma pelouse est arrosée.
: Ma pelouse est arrosée.
Ces propositions sont susceptibles d’être vraies ou fausses. Mais au regard de celles-ci, on constate que
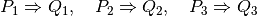
Ce qui peut se lire de différentes façons:
 implique
implique 
Si la proposition
 est vraie, alors la proposition
est vraie, alors la proposition  est vraie (si
est vraie (si  , alors
, alors  )
)La proposition
 est vraie seulement si la proposition
est vraie seulement si la proposition
 est vraie (
est vraie ( seulement si
seulement si  )
)La proposition
 est une condition nécessaire à la
réalisation de la proposition
est une condition nécessaire à la
réalisation de la proposition  (
( est CN à
est CN à
 )
)
L’implication est transitive, ce qui veut dire que si  et que
et que 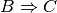 ,alors
,alors 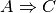 .
.
Réciproque¶
La réciproque de l’implication 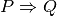 est l’implication
est l’implication
 . Ce qu’on peut lire de différentes façons:
. Ce qu’on peut lire de différentes façons:
 implique
implique 
La proposition
 est vraie si la proposition
est vraie si la proposition  est
vraie (
est
vraie ( si
si  )
)La proposition
 est une condition suffisante à la
réalisation de la proposition
est une condition suffisante à la
réalisation de la proposition  (
( est CS à
est CS à
 )
)
Ce n’est pas parce qu’une implication est vraie que sa réciproque l’est aussi. Dans les trois exemples considérés :
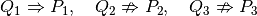
Ce n’est pas parce que “ma pelouse est arrosée” que cela est du à la pluie. L’arrosage peut être artificiel. Ce n’est pas parce qu’un nombre (6 par exemple) est multiple de 2, qu’il est multiple de 4.
Contraposée¶
Si on note 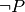 , la négation de la proposition
, la négation de la proposition  , la
contraposée de
, la
contraposée de 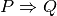 est
est
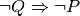 . On nie donc les affirmations
. On nie donc les affirmations  et
et  et on renverse le sens de l’implication. Si une implication
est vraie, la contraposée est vraie également, ce qui fait bien
comprendre le sens de la condition nécessaire. Par exemple, comme
“
et on renverse le sens de l’implication. Si une implication
est vraie, la contraposée est vraie également, ce qui fait bien
comprendre le sens de la condition nécessaire. Par exemple, comme
“ est un naturel multiple de 4”, implique que “
est un naturel multiple de 4”, implique que “ est un
naturel multiple de 2”; si
est un
naturel multiple de 2”; si  n’est pas multiple de 2, il n’est
certainement pas multiple de 4. Ou encore si “ma pelouse n’est pas
arrosée”, c’est nécessairement “qu’il ne pleut pas”.
n’est pas multiple de 2, il n’est
certainement pas multiple de 4. Ou encore si “ma pelouse n’est pas
arrosée”, c’est nécessairement “qu’il ne pleut pas”.
Équivalence¶
Dans les cas où

on parde d’équivalence et on note
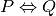
Ce qu’on peut lire de différentes façons:
Les propositions
 et
et  sont équivalentes
sont équivalentesLa proposition
 est vraie si et seulement si la proposition
est vraie si et seulement si la proposition
 est vraie (
est vraie ( si et seulement si
si et seulement si  )
)La proposition
 est une condition nécessaire et suffisante à
la réalisation de la proposition
est une condition nécessaire et suffisante à
la réalisation de la proposition  (
( est CNS à
est CNS à
 )
)
2. Démonstration¶
Démontrer consiste à déduire qu’une proposition appelée thèse est vraie, en partant de propositions appelées hypothèses que l’on suppose être vraies le temps de la démonstration. Pour démontrer, on s’appuie également sur des propositions mathématiques qui sont vraies parce qu’elles sont admises comme telles ou parce qu’elles ont été démontrées auparavant. Les propositions admises sont des axiomes, celles qui sont démontrées sont des théorèmes.
Soit à démontrer que 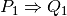 .
.
Hypothèses : 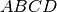 est un quadrilatère (sous-entendu plan) Les
diagonales
est un quadrilatère (sous-entendu plan) Les
diagonales  se coupent en leur milieu.
se coupent en leur milieu.
Thèse : 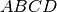 est un parallélogramme
est un parallélogramme
La thèse se réfère à la définition de parallélogramme comme étant un quadrilatère formé de deux paires de côtés parallèles. La démonstration repose sur diverses propriétés comme un axiome, le premier cas d’isométrie des triangles (Côté-Angle-Côté) et un théorème qui dit que si deux droites coupent une troisième en formant des angles alternes internes de même amplitude, alors elles sont parallèles.
Pour prouver une équivalence comme 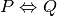 , on
démontre souvent les deux implications l’une après l’autre.
, on
démontre souvent les deux implications l’une après l’autre.
Comme nous l’avons déjà mentionné, 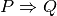 est la
Condition Nécessaire. Ce qui exprime que si
est la
Condition Nécessaire. Ce qui exprime que si  n’est pas vraie,
n’est pas vraie,
 ne l’est pas non plus. Tandis que
ne l’est pas non plus. Tandis que  est
la Condition Suffisante. Ce qui exprime que
est
la Condition Suffisante. Ce qui exprime que  vraie suffit à
rendre
vraie suffit à
rendre  vraie.
vraie.
Pièges¶
Par essence, la démonstration est déductive et les étapes se succèdent en respectant les règles logiques, ce que certains appellent l’hygiène du mathématicien.
Un premier piège pour le débutant consiste à utiliser la thèse dans la démonstration. C’est-à-dire qu’on utilise le résultat pour le prouver. Dans l’exemple du quadrilatère qui a des diagonales qui se coupent en leur milieu, il n’est pas rare de voir un apprenti géomètre se servir erronément du parallélisme de deux côtés pour en déduire que des angles alternes internes ont même amplitude et que des côtés sont parallèles…
Un autre piège consiste à affirmer une chose et son contraire au sein de la même démonstration. Le principe de non-contradiction est à la base de toute théorie mathématique. Aristore l’aurait formulé sous la forme : “il est impossible qu’une seule et même chose soit, et tout à la fois ne soit pas, à une même autre chose, sous le même rapport”.
Des négations particulières méritent notre attention. Pour prouver
qu’une propriété n’est pas vraie pour toutes les valeurs de 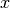 ,
il suffit de trouver une valeur de
,
il suffit de trouver une valeur de 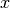 pour laquelle la propriété
n’est pas satisfaite. En mathématiques, cela se passe très différemment
de ce qu’on observe dans de nombreux domaines de la vie courante où il
faut de nombreux contre exemples pour faire tomber une vérité. Par
ailleurs, pour nier qu’une propriété qui est vraie pour une valeur de
pour laquelle la propriété
n’est pas satisfaite. En mathématiques, cela se passe très différemment
de ce qu’on observe dans de nombreux domaines de la vie courante où il
faut de nombreux contre exemples pour faire tomber une vérité. Par
ailleurs, pour nier qu’une propriété qui est vraie pour une valeur de
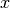 , il suffit de prouver que pour toutes les valeurs de
, il suffit de prouver que pour toutes les valeurs de 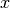 la propriété n’est pas satisfaite.
la propriété n’est pas satisfaite.
Envisageons maintenant différents types de démonstration…
Directe¶
Cela consiste à démontrer la proposition énoncée en partant directement des hypothèses données pour en arriver à la thèse par une suite d’implications logiques.
Pour prouver que  , sachant que
, sachant que
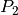 est l’hypothèse et que
est l’hypothèse et que  est la thèse,
commençons par traduire l’hypothèse :
est la thèse,
commençons par traduire l’hypothèse :
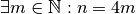
Ce qui veut encore dire que
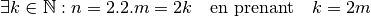
Ce qui prouve la thèse, à savoir que  est un multiple de 2.
est un multiple de 2.
Par l’absurde¶
Cela consiste à supposer le contraire de la proposition énoncée et de montrer qu’on aboutit alors à une contradiction ou impossibilité.
Pour prouver que le nombre 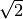 est irrationnel, on suppose
que ce n’est pas le cas, c’est-à-dire qu’il peut s’exprimer sous forme
de fraction de naturels:
est irrationnel, on suppose
que ce n’est pas le cas, c’est-à-dire qu’il peut s’exprimer sous forme
de fraction de naturels:
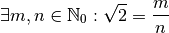
Il en résulte que

Ce qui veut dire que 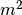 est pair. Mais le carré d’un naturel
pair est pair et inversement. D’où il existe un naturel
est pair. Mais le carré d’un naturel
pair est pair et inversement. D’où il existe un naturel  tel
que
tel
que 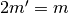 ,
,  et l’égalité (1) devient
et l’égalité (1) devient
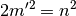
Il en résulte que 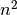 est pair. Mais le carré d’un naturel pair
est pair et inversement. D’où il existe un naturel
est pair. Mais le carré d’un naturel pair
est pair et inversement. D’où il existe un naturel 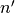 tel que
tel que
 ,
,  et l’égalité (2) devient
et l’égalité (2) devient
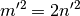
Et ainsi de suite… Indéfiniment. Ce qui n’est pas possible puisque
 et
et 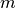 sont naturels et limités, on ne peut pas les
diviser indéfiniment par 2. Il faut donc rejeter l’hypothèse faite à
savoir que
sont naturels et limités, on ne peut pas les
diviser indéfiniment par 2. Il faut donc rejeter l’hypothèse faite à
savoir que 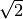 puisse être rationnel.
puisse être rationnel.
Par contraposée¶
Démontrer que 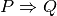 , c’est équivalent à démontrer que
, c’est équivalent à démontrer que
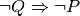 .
.
Pour démontrer que “Si le dernier chiffre d’un nombre naturel  est 2 alors
est 2 alors  n’est pas le carré d’un entier”, on peut démontrer
que si
n’est pas le carré d’un entier”, on peut démontrer
que si  est le carré d’un naturel alors son dernier chiffre
n’est pas 2. En effet, si
est le carré d’un naturel alors son dernier chiffre
n’est pas 2. En effet, si 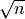 se termine
se termine
par 1 ou 9, son carré se termine par 1.
par 2 ou 8, son carré se termine par 4.
par 3 ou 7, son carré se termine par 9.
par 2 ou 8, son carré se termine par 4.
par 4 ou 6, son carré se termine par 6.
par 5, son carré se termine par 5.
par 0, son carré se termine par 0.
Et jamais un carré ne se termine par 2.
Par récurrence¶
Pour prouver qu’une propriété 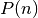 est vraie
est vraie
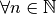 , on démontre qu’elle est vraie pour
, on démontre qu’elle est vraie pour
 et que si elle est vraie pour
et que si elle est vraie pour  , cela implique
qu’elle est vraie pour
, cela implique
qu’elle est vraie pour 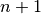 .
.
Soit à démontrer par exemple que la somme des carrés des  premiers naturels est égale à
premiers naturels est égale à 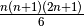 ,
c’est-à-dire que
,
c’est-à-dire que

Pour  , la propriété est vraie car
, la propriété est vraie car
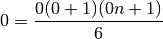
Si la propriété est vraie pour  , alors
, alors
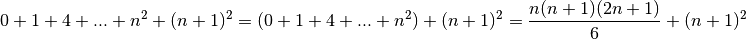
Si on réduit au même dénominateur les deux termes du dernier membre de
l’égalité, puis qu’on met  en évidence, on obtient
en évidence, on obtient

On peut factoriser 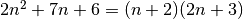 et finalement obtenir
et finalement obtenir
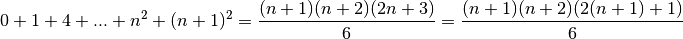
Ce qui prouve que l’égalité est vraie pour 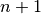 .
.
