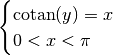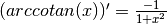Théorie¶
Les fonctions réciproques¶
1. Rappels¶
Une fonction est une relation entre deux ensembles telle que chaque nombre ait maximum une image.
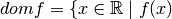 existe
existe 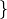
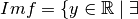 au moins un
au moins un 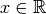 pour lequel
pour lequel 
Pour que la réciproque de
 soit une fonction, il faut qu’à chaque élément de
soit une fonction, il faut qu’à chaque élément de  corresponde un seul élément du domaine de
corresponde un seul élément du domaine de  .
.
Si ce n’est pas le cas, il faut restreindre le domaine de  pour la rendre bijective ( c-à-d qu’à chaque élément du domaine corresponde un seul élément de l’ensemble image et réciproquement).
pour la rendre bijective ( c-à-d qu’à chaque élément du domaine corresponde un seul élément de l’ensemble image et réciproquement).
2. Définition¶
Si  est une bijection de A vers B (avec A
est une bijection de A vers B (avec A 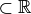 et B
et B 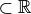 )
)
alors 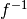 existe et est une bijection de B vers A telle que si
existe et est une bijection de B vers A telle que si 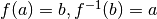 .
.
Le graphe d’une réciproque s’obtient dans un repère orthonormé par une symétrie orthogonale d’axe 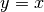 , ce qui a pour effet d’inverser les axes et d’envoyer un point (a,b) sur un point (b,a).
, ce qui a pour effet d’inverser les axes et d’envoyer un point (a,b) sur un point (b,a).
Pour trouver l’ équation d’une réciproque, on intervertit 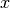 et
et 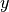 dans l’expression de
dans l’expression de 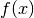 et on résout l’équation en
et on résout l’équation en 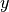 .
.
Attention: l’exposant -1 a 2 significations; c’est le contexte qui précise si 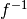 est l’inverse ou la réciproque de
est l’inverse ou la réciproque de  . C’est ce dernier sens qui est le plus fréquent.
. C’est ce dernier sens qui est le plus fréquent.
3. Dérivée d’une fonction réciproque¶
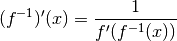
On peut démontrer ce résultat
algébriquement, en utilisant le fait que la composée d’une fonction et de sa réciproque est l’identité et en dérivant les deux membres de l’égalité.
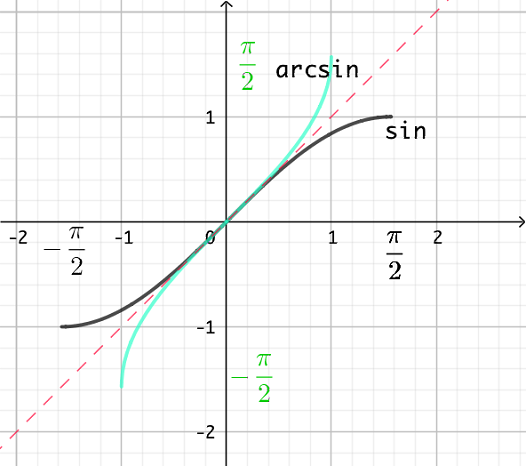
géométriquement, en utilisant le fait que, les deux graphes étant symétriques, leurs tangentes à des points correspondants le sont aussi et donc que leurs pentes sont inverses.

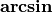 :
: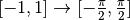
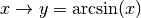 tel que
tel que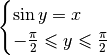
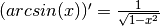
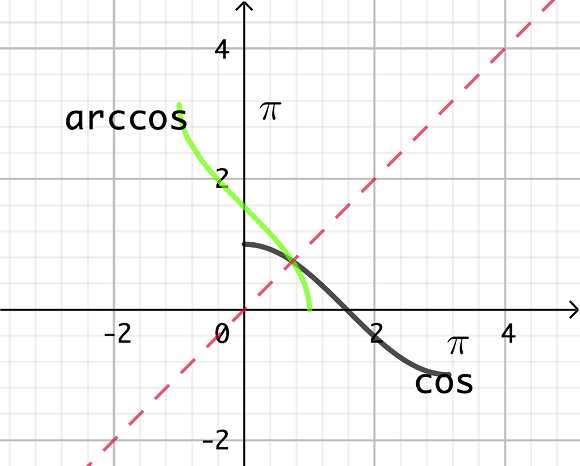
 :
: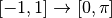
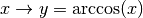 tel que
tel que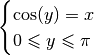
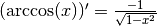
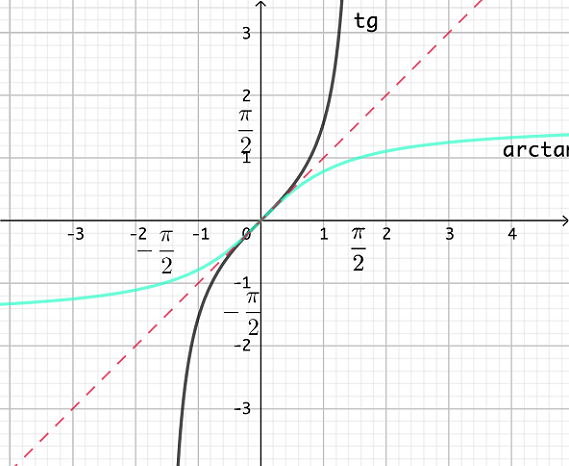
 :
: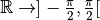
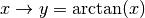 tel que
tel que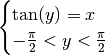
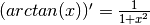
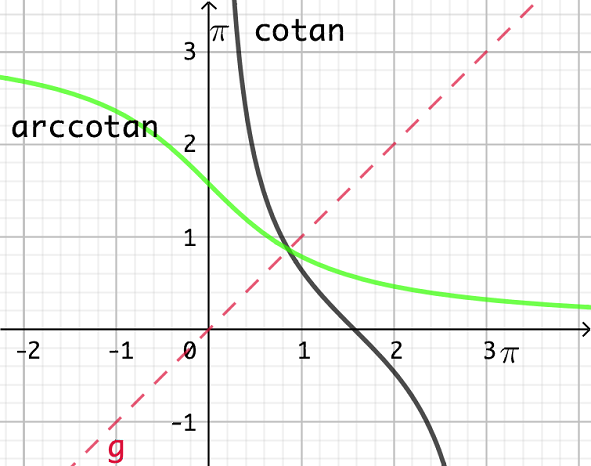
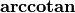 :
: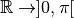
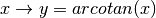 tel que
tel que