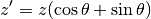Théorie¶
1. Propriétés élémentaires¶
Nouveaux nombres¶
L’équation 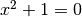 n’a pas de solution dans l’ensemble des réels
parce qu’il n’y a pas de réel dont le carré vaut -1. Il suffit
d’imaginer que ce nombre existe… Ce nombre est un imaginaire noté
n’a pas de solution dans l’ensemble des réels
parce qu’il n’y a pas de réel dont le carré vaut -1. Il suffit
d’imaginer que ce nombre existe… Ce nombre est un imaginaire noté
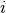 . L’équation a alors pour solution
. L’équation a alors pour solution 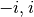 . Et du fait que
le carré de
. Et du fait que
le carré de 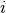 vaut -1, on peut déduire que
vaut -1, on peut déduire que

Forme algébrique¶
Un nombre complexe est tout de même plus élaboré que ce simple
imaginaire i. On veut que 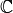 , l’ensemble des nombres
complexes, prolonge
, l’ensemble des nombres
complexes, prolonge 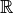 , l’ensemble des nombres réels.
Tout réel
, l’ensemble des nombres réels.
Tout réel  doit donc être un complexe. On veut encore qu’en
multipliant un complexe par un complexe, ce soit un complexe. Ainsi en
multipliant le réel
doit donc être un complexe. On veut encore qu’en
multipliant un complexe par un complexe, ce soit un complexe. Ainsi en
multipliant le réel 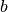 (qui est complexe) par l’imaginaire pur
(qui est complexe) par l’imaginaire pur
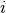 , on obtient le complexe
, on obtient le complexe 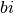 . On veut enfin qu’en
additionnant deux complexes, on obtienne un complexe. Ainsi en
additionnant le réel
. On veut enfin qu’en
additionnant deux complexes, on obtienne un complexe. Ainsi en
additionnant le réel  (qui est complexe) au complexe
(qui est complexe) au complexe
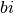 , on obtient le complexe
, on obtient le complexe  .
.
La forme générale d’un complexe est
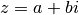
 étant la partie réelle de
étant la partie réelle de  (notée
(notée 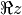 ) et
) et
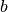 la partie imaginaire de
la partie imaginaire de  (notée
(notée  ),
),
 et
et 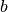 tous deux réels.
tous deux réels.
Deux complexes sont égaux s’ils ont même partie réelle et même partie imaginaire.
Opérations¶
Considérons deux complexes 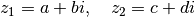 , on
définit assez naturellement l’addition et la multiplication:
, on
définit assez naturellement l’addition et la multiplication:
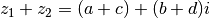

Le neutre pour l’addition est 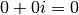 . Le symétrique de
. Le symétrique de
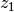 pour l’addition est tout simplement
pour l’addition est tout simplement
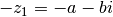
Le neutre pour la multiplication est 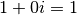 . Pour obtenir le
symétrique de
. Pour obtenir le
symétrique de 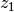 pour la multiplication, c’est-à-dire
l’inverse, il faut trouver le complexe
pour la multiplication, c’est-à-dire
l’inverse, il faut trouver le complexe 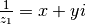 tel
que
tel
que
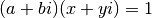
Ou encore
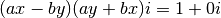
C’est-à-dire que
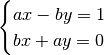
Ce système de deux équations à deux inconnues a une solution unique si
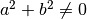 , ce qui est le cas pour tout complexe sauf pour
, ce qui est le cas pour tout complexe sauf pour
 . À cette condition, la solution du système est
. À cette condition, la solution du système est
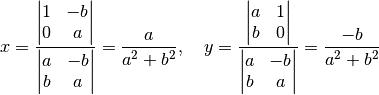
Et
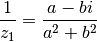
On montre sans difficultés que  et
et
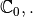 sont des groupes commutatifs et que
sont des groupes commutatifs et que
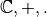 est un champ.
est un champ.
Forme trigonométrique¶
Dans un repère orthonormé du plan, on peut associer un point à tout
couple de réels. Ainsi, au complexe  , on peut associer le
point
, on peut associer le
point  de coordonnées
de coordonnées 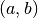 (figure 1). On parle de
plan de Gauss dans ce cas, d’axe réel pour l’axe des abscisses et d’axe
imaginaire pour l’axe des ordonnées.
(figure 1). On parle de
plan de Gauss dans ce cas, d’axe réel pour l’axe des abscisses et d’axe
imaginaire pour l’axe des ordonnées.
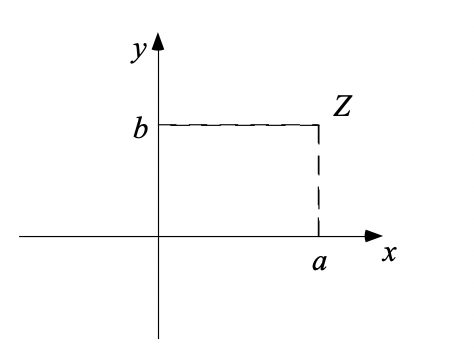
Figure 1¶
Si dans le plan de Gauss, on associe un point  au complexe
au complexe
 , on peut encore y associer le vecteur ayant l’origine des axes
pour origine et
, on peut encore y associer le vecteur ayant l’origine des axes
pour origine et  pour extrémité (figure 2). Ce vecteur a une
longueur
pour extrémité (figure 2). Ce vecteur a une
longueur  et détermine un certain angle
et détermine un certain angle  avec
l’axe des abscisses.
avec
l’axe des abscisses.
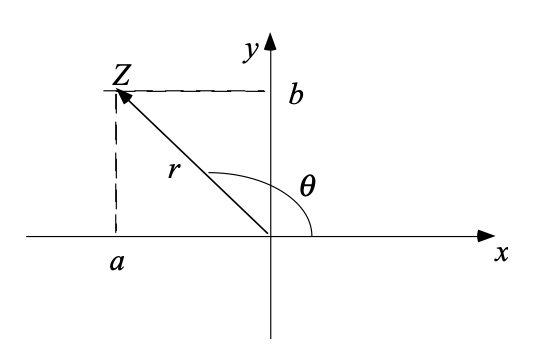
Figure 2¶
On voit sans difficultés que
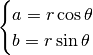
Inversement,

Et on peut écrire que
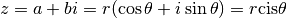
Il s’agit de la forme trigonométrique d’un complexe:  est le
module de
est le
module de  , on le note également
, on le note également 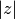 ;
;
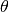 est l’argument de
est l’argument de  .
.
Conjugué¶
Le conjugué du complexe  est le complexe
est le complexe
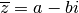 . Dans le plan de Gauss, à un complexe et son
conjugué correspondent des points qui sont symétriques par rapport à
l’axe
. Dans le plan de Gauss, à un complexe et son
conjugué correspondent des points qui sont symétriques par rapport à
l’axe 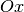 . On peut vérifier sans difficultés que
. On peut vérifier sans difficultés que
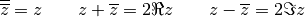
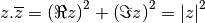
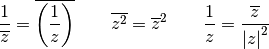
Si  et
et 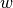 sont deux complexes, on peut montrer que
sont deux complexes, on peut montrer que
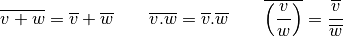
Inégalité triangulaire¶
Dans le plan de Gauss, deux complexes  et
et 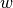 étant
associés à des vecteurs de même origine, on peut considérer qu’ils
déterminent un triangle. L’inégalité triangulaire peut donc se traduire
sous forme de complexes et on a
étant
associés à des vecteurs de même origine, on peut considérer qu’ils
déterminent un triangle. L’inégalité triangulaire peut donc se traduire
sous forme de complexes et on a

Le module de la somme de deux complexes est plus petit que la somme des modules. Le module de la différence de deux complexes est plus grand que la différence des modules.
Produit et quotient¶
En utilisant les formules trigonométriques de  et
et
 on démontre sans difficulté que si
on démontre sans difficulté que si
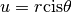 et
et 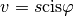 , alors
, alors

Ce qui veut dire que pour multiplier deux complexes, on multiplie les modules et on additionne les arguments, tandis que pour en faire le quotient, on fait le quotient des modules et on soustrait les arguments.
2. Transformations planes¶
Translations¶
Soit  un complexe associé au point
un complexe associé au point 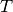 du plan de
Gauss. On considère la translation de vecteur
du plan de
Gauss. On considère la translation de vecteur
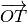 où
où 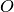 est l’origine du repère. Le
point quelconque
est l’origine du repère. Le
point quelconque  est envoyé par cette translation sur le point
est envoyé par cette translation sur le point
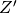 associé au complexe
associé au complexe 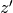 (figure 3) et
(figure 3) et
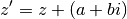

Figure 3¶
3. Racines¶
Formule de Moivre¶
Démontrons par récurrence que pour  naturel
naturel
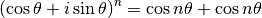
Pour 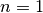 , c’est évident.
, c’est évident.
Si la propriété est vraie pour  , alors
, alors
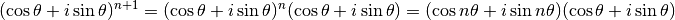
En distribuant le dernier membre de l’égalité, on a
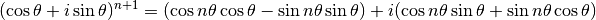
En utilisant les formules trigonométriques de 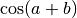 et
et
 , cela devient
, cela devient
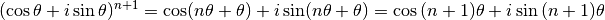
La propriété est donc vraie pour  .
.
Racine carrée par voie algébrique¶
Trouver algébriquement les racines carrées d’un nombre complexe
 (
( et
et  réels), c’est trouver les réels
réels), c’est trouver les réels
 et
et 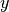 qui satisfont l’équation
qui satisfont l’équation
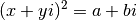
Ou encore
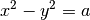

En élevant ces deux égalités au carré et en les additionnant membre à membre, on obtient successivement
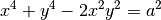
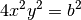
En additionnant membre à membre les deux égalités précédentes, on a

On en déduit que
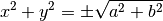
Il faut cependant rejeter le cas négatif.
Des équations (1) et (3), on tire les valeurs de x et y

Pour savoir quel signe choisir, on retourne à l”équation (2). Si
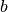 est positif, les parties réelle et imaginaire des racines
carrées doivent être de même signe et les racines carrées de
est positif, les parties réelle et imaginaire des racines
carrées doivent être de même signe et les racines carrées de
 sont
sont
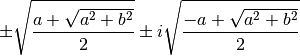
Si 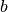 est négatif, les parties réelle et imaginaire des racines
carrées doivent être de signes contraires et les racines carrées de
est négatif, les parties réelle et imaginaire des racines
carrées doivent être de signes contraires et les racines carrées de
 sont
sont

Racine  -ièmes¶
-ièmes¶
Pour trouver les racines  -ièmes (
-ièmes ( naturel) d’un nombre
complexe, il est plus simple de l’écrire sous forme trigonométrique.
Ainsi, trouver les racines
naturel) d’un nombre
complexe, il est plus simple de l’écrire sous forme trigonométrique.
Ainsi, trouver les racines  -ièmes du nombre complexe
-ièmes du nombre complexe
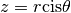 , c’est trouver les complexes
, c’est trouver les complexes
 tels que
tels que

Par la formule de Moivre, on a
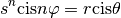
Pour que deux complexes soient égaux, ils doivent avoir mêmes modules et mêmes arguments. Dès lors
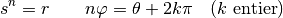
Ce qui veut dire que
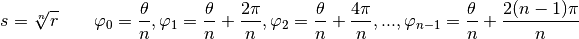
On constate que si on donne d’autres valeurs à 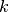 que les valeurs
0,1, …,
que les valeurs
0,1, …,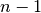 , on en revient à des racines déjà reprises. Un
complexe (et un réel en particulier) a donc
, on en revient à des racines déjà reprises. Un
complexe (et un réel en particulier) a donc  racines
racines
 -ièmes complexes (dont certaines peuvent être réelles).
-ièmes complexes (dont certaines peuvent être réelles).
Sachant que toutes ces racines ont même module et des arguments en suite
arithmétique de raison 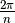 , elles forment un polygone
régulier à
, elles forment un polygone
régulier à  côtés (quand
côtés (quand 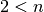 ) dans le plan de Gauss.
Ces racines forment également une suite géométrique de raison
) dans le plan de Gauss.
Ces racines forment également une suite géométrique de raison
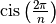 car
car

Au paragraphe précédent nous avons vu comment calculer les racines
carrées à partir de la forme algébrique d’un complexe. Par ce que nous
venons de voir pour les racines  -ièmes, on peut aussi les
calculer à partir de leur forme trigonométrique. Les deux racines
carrées du complexe
-ièmes, on peut aussi les
calculer à partir de leur forme trigonométrique. Les deux racines
carrées du complexe 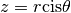 sont
sont

4. Équations du second degré¶
À coefficients réels¶
Considérons tout d’abord une équation à coefficients réels
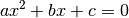
On sait que dans 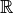 , elle a deux solutions distinctes
quand le réalisant
, elle a deux solutions distinctes
quand le réalisant  est strictement positif et
une solution double quand
est strictement positif et
une solution double quand  est nul. Si
est nul. Si  est
négatif, alors
est
négatif, alors 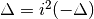 et l’équation a deux
racines complexes
et l’équation a deux
racines complexes
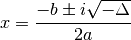
À coefficients complexes¶
Si l’équation du second degré 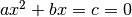 est à coefficient
complexes, on la résout de la même manière qu’une équation à
coefficients réels et on obtient les solutions
est à coefficient
complexes, on la résout de la même manière qu’une équation à
coefficients réels et on obtient les solutions

où 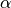 et
et  sont les racines carrées du complexe
sont les racines carrées du complexe
 .
.

 . Le point quelconque
. Le point quelconque 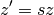

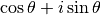 un complexe associé au point
un complexe associé au point
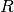 du plan de Gauss. On considère la rotation de centre
du plan de Gauss. On considère la rotation de centre