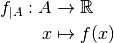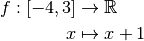2 Fonctions continues¶
2.1 Définition et exemples¶
Définition 2.1.1. Soit  un intervalle éventuellement privé d’un point. Soit
un intervalle éventuellement privé d’un point. Soit
 .
.
On dit que
est une fonction continue en
si et seulement si pour tout
, il existe
tel que pour tout
tel que
, on a
.
Remarque 2.1.2. Cette définition, assez technique, ne doit pas vous faire peur. Une
lecture intuitive de cette définition est la suivante : si un
processus  qui dépend d’une variable
qui dépend d’une variable  est continu
autour d’une certaine valeur de
est continu
autour d’une certaine valeur de  qui vaut
qui vaut  , alors je
dois pouvoir approcher les valeurs de
, alors je
dois pouvoir approcher les valeurs de 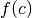 autant que je le
souhaite si je suis capable d’approcher la valeur de
autant que je le
souhaite si je suis capable d’approcher la valeur de  autant
que nécessaire.
Il est recommandé d’appliquer cette définition sur les deux exemples
suivants afin d’analyser celle-ci en profondeur et comprendre en quoi
elle formalise l’idée intutive de continuité.
autant
que nécessaire.
Il est recommandé d’appliquer cette définition sur les deux exemples
suivants afin d’analyser celle-ci en profondeur et comprendre en quoi
elle formalise l’idée intutive de continuité.
Exemple 2.1.3.
 définie sur
définie sur
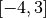 . En effet, quelle que soit l’erreur maximale autorisée
. En effet, quelle que soit l’erreur maximale autorisée
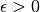 , quitte à sélectionner des valeurs pour
, quitte à sélectionner des valeurs pour  assez proche de
assez proche de  (à une distance de
(à une distance de  d’au plus
d’au plus
 ), les valeurs
), les valeurs  approcheront bien la
valeur
approcheront bien la
valeur 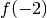 avec une erreur plus petite ou égale à
avec une erreur plus petite ou égale à
 .
. et que le graphe peut être réalisé d’un seul
trait.
et que le graphe peut être réalisé d’un seul
trait.Exemple 2.1.4.
 définie sur
définie sur
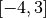 . En effet, en prenant comme erreur maximale autorisée
. En effet, en prenant comme erreur maximale autorisée
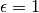 , il est impossible de trouver un
, il est impossible de trouver un  tel qu’à toutes les valeurs de
tel qu’à toutes les valeurs de  possibles à une distance au
plus
possibles à une distance au
plus 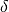 de
de  , la fonction
, la fonction  associera un
nombre
associera un
nombre  dont la distance avec
dont la distance avec 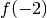 est plus
petite que
est plus
petite que  . La raison étant que juste à gauche de
. La raison étant que juste à gauche de  , la fonction prend des valeurs strictement négative alors que
, la fonction prend des valeurs strictement négative alors que
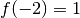 .
. et que le graphe ne peut pas être réalisé d’un seul trait.
et que le graphe ne peut pas être réalisé d’un seul trait.Remarque 2.1.5. Une caractérisation intuitive des graphes de fonctions continues est qu’il s’agit des fonctions dont le graphe peut être tracé d’un seul trait. Néanmoins, celle-ci est imprécise et peut mener à des erreurs, puisque la continuité ne concerne que les sauts dans les valeurs d’une fonction (autrement dit : les sauts verticaux dans le graphe de la fonction) et non son domaine de définition (les sauts horizontaux dans le graphe de la fonction). Permettons-nous d’insister : il ne fait pas sens de parler de continuité d’une fonction en un point où elle n’est pas définie ! Par exemple, la fonction inverse :
Cette fonction est bien partout continue ! Il ne fait pas sens
d’affirmer qu’elle est discontinue en  , puisqu’elle n’est même
pas définie en
, puisqu’elle n’est même
pas définie en  .
.
Définition 2.1.6. Soit  un intervalle éventuellement privé d’un point. Soit
un intervalle éventuellement privé d’un point. Soit  .
.
On dit que
est une fonction continue si elle est continue en tous les points de son domaine de définition.
Exercice 2.1.7. Donner le domaine de définition des fonctions dont les graphes sont les suivants, puis déterminer si elles sont continues ou non. Si elles ne sont pas continues, donner l’ensemble des points où elles sont discontinues.










2.2 Continuité des fonctions de référence¶
Théorème 2.2.1. Toutes les fonctions de référence sont continues.
Démonstration Pas en math 4. 1
Remarque 2.2.2. De toutes les fonctions de référence, seule la fonction inverse n’a pas
un graphe qui peut être tracé d’un seul trait . À nouveau, il s’agit
dans ce cas d’une question de domaine (la fonction inverse n’est pas
définie en  puisqu’il ne fait pas sens de diviser par
puisqu’il ne fait pas sens de diviser par
 ) et non de continuité.
) et non de continuité.
Exemple 2.2.3. Par exemple, la fonction racine cubique est continue :
2.3 Propriétés des fonctions continues¶
Commençons avec un exemple :
Exemple 2.3.1. Considérons les deux fonctions :
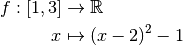
et

dont les graphes sont les suivants :
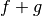 ? Au niveau des graphes, cela
revient à additionner les ordonnées des points des graphes de
? Au niveau des graphes, cela
revient à additionner les ordonnées des points des graphes de
 et
et  qui ont la même abscisse.
qui ont la même abscisse.Sans surprise, aucune discontinuité n’est apparue. En additionnant deux fonctions continues, on a obtenu une nouvelle fonction continue. Ce n’est pas un hasard, comme l’indique la proposition suivante.
Proposition 2.3.2. Soit  un intervalle éventuellement privé d’un point. Soient
un intervalle éventuellement privé d’un point. Soient
 et
et  deux
fonctions continues. Alors :
deux
fonctions continues. Alors :
La fonction
 est continue.
est continue.La fonction
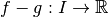 est continue.
est continue.La fonction
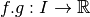 est continue.
est continue.La fonction
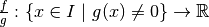 est
continue.
est
continue.
Démonstration Pas en math 4. Voir annexe pour les curieux.
De manière éventuellement plus surprenante, la composée de deux fonctions continues (compatibles) est également toujours une fonction continue :
Proposition 2.3.3. Soit 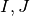 deux intervalles. Soient
deux intervalles. Soient
 et
et  deux
fonctions continues telle que
deux
fonctions continues telle que
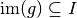 . Alors :
. Alors :
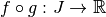 est continue.
est continue.
Démonstration Pas en math 4.
Une dernière opération qui conserve la continuité est la restriction :
Définition 2.3.4. Soit  un intervalle éventuellement privé d’un point. Soit
un intervalle éventuellement privé d’un point. Soit
 .
Soit
.
Soit  . Alors la restriction de
. Alors la restriction de  sur
sur
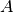 est la fonction :
est la fonction :
Exemple 2.3.5. Soit la fonction :
dont le graphe est :
La restriction de  sur, par exemple,
sur, par exemple,
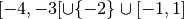 , est la fonction :
, est la fonction :
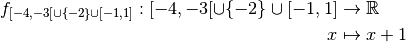
et son graphe est :
Comme annoncé, la restriction d’une fonction continue est toujours continue :
Proposition 2.3.6. Soit  un intervalle éventuellement privé d’un point.
Soit
un intervalle éventuellement privé d’un point.
Soit  une fonction continue. Soit
une fonction continue. Soit
 .
Alors la restriction de
.
Alors la restriction de  sur
sur 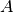 est continue.
est continue.
Démonstration Pas en math 4. Notons néanmoins que la démonstration est extrêment simple.
Grâce au théorème 2.2.1, nous savons que toutes les fonctions de référence sont continues. Or, les propositions 2.3.2, 2.3.3 et 2.3.6 nous disent que lorsqu’on combine deux fonctions continues selon une des opérations sur les fonctions les plus simples, nous pouvons être certains que le résultat est lui aussi une fonction continue. Ainsi, nous sommes à présent capables de justifier la continuité de nombreuses fonctions.
Exercice 2.3.7. Les fonctions suivantes sont-elles continues ? Si oui, justifier. Si non, faire le graphe de la fonction et donner l’ensemble des points de discontinuité.








2.4 Grands théorèmes des fonctions continues (optionnel)¶
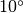 à minuit et
qu’elle est de
à minuit et
qu’elle est de 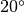 à midi et qu’on choisit une
température en
à midi et qu’on choisit une
température en 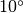 et
et 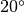 , par exemple
, par exemple
 , on est intuitivement convaincu qu’il y a eu au
moins un court instant dans la matinée où la température de la pièce
était de
, on est intuitivement convaincu qu’il y a eu au
moins un court instant dans la matinée où la température de la pièce
était de  (puisque le phénomène est continu, on doit
bien passer par toutes les valeurs intermédiaires entre
(puisque le phénomène est continu, on doit
bien passer par toutes les valeurs intermédiaires entre
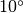 et
et 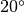 pour passer de
pour passer de
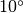 à
à 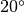 ). Cette intuition est
formalisée par le théorème suivant :
). Cette intuition est
formalisée par le théorème suivant :Théorème 2.4.1 (Théorème des valeurs intermédiaires). Soit  un intervalle de la forme
un intervalle de la forme 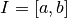 . Soit
. Soit
 une fonction continue.
Pour tout
une fonction continue.
Pour tout 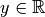 compris entre
compris entre 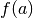 et
et
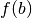 , il existe
, il existe 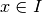 tel que
tel que 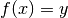 .
.
Démonstration Pas en math 4. 2
Exemple 2.4.2. Considérons la fonction suivante qui est la restriction de la fonction
carrée sur 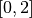 .
.
Puisque cette fonction est continue, 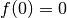 ,
, 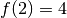 et
et
 , on peut être certain qu’il existe une abscisse
, on peut être certain qu’il existe une abscisse
 entre
entre  et
et  telle que la valeur de cette
fonction en
telle que la valeur de cette
fonction en  vaut exactement
vaut exactement 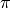 (dans ce cas-ci, il
est possible de déterminer ce
(dans ce cas-ci, il
est possible de déterminer ce  (qui est ici unique) :
(qui est ici unique) :
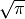 ).
).
Remarque 2.4.3. Le théorème n’affirme pas que l’abscisse  telle que
telle que
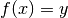 est unique ! Comme le montre l’exemple suivant (où on
choisit pour
est unique ! Comme le montre l’exemple suivant (où on
choisit pour 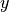 l’ordonnée
l’ordonnée  , qui se trouve entre
, qui se trouve entre
 et
et 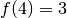 ), il peut y avoir plusieurs abscisses
de cette sorte :
), il peut y avoir plusieurs abscisses
de cette sorte :
La fonction vaut  en
en  , en
, en  et en
et en  .
.
Théorème 2.4.4. Soit  un intervalle de la forme
un intervalle de la forme 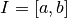 . Soit
. Soit
 une fonction continue.
une fonction continue.
 est nécessairement bornée et atteint ses bornes, autrement
dit
est nécessairement bornée et atteint ses bornes, autrement
dit  a un point de minimum et un point de maximum.
a un point de minimum et un point de maximum.
Démonstration Pas en math 4. 3
Remarque 2.4.5. Dans le prochain chapitre, nous nous intéresserons beaucoup aux (points de) minimum et maximum d’une fonction. Ce théorème des bornes atteintes nous dit que pour une fonction continue définie sur un intervalle fermé, nous pouvons être certain qu’un point de minimum et qu’un point de maximum existe, mais il ne nous dit pas comment les trouver.
Remarque 2.4.6. La fonction dont le graphe est ci-dessous est définie sur un intervalle
de la forme 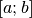 et est continue :
et est continue :
Il s’agit de la fonction :

Nous serions bien incapables (à ce stade) de déterminer quel est le (point de) maximum et le (point de) minimum de cette fonction, mais nous sommes certains que ceux-ci existent bel et bien (visuellement, on les identifie immédiatement sans pour autant être capable de les déterminer exactement).
2.5 Prolongements continus¶
Exemple 2.5.1. Voici le graphe d’une fonction définie sur
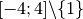 qui est continue :
qui est continue :
Il ne fait pas sens de dire qu’elle est discontinue (ou continue) en
 puisqu’elle n’est pas définie en
puisqu’elle n’est pas définie en  .
.
Exemple 2.5.2. Voici le graphe d’une autre fonction définie sur
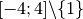 qui est continue :
qui est continue :
Il ne fait pas sens de dire qu’elle est continue (ou discontinue) en
 puisqu’elle n’est pas définie en
puisqu’elle n’est pas définie en  .
.
 de sorte que le résultat final soit continu,
même en
de sorte que le résultat final soit continu,
même en  . Par contre, pour la deuxième fonction, il est
possible de trouver un tel prolongement continu : il suffit d’étendre
la fonction en la définissant en
. Par contre, pour la deuxième fonction, il est
possible de trouver un tel prolongement continu : il suffit d’étendre
la fonction en la définissant en  en décidant que le
prolongement de la fonction vaut
en décidant que le
prolongement de la fonction vaut  en
en  . Cette
intuition correspond au fait que la deuxième fonction possède un
prolongement continu tandis que la première non.
. Cette
intuition correspond au fait que la deuxième fonction possède un
prolongement continu tandis que la première non.Définition 2.5.3. Soit un intervalle  et soit
et soit 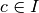 . Soit
. Soit 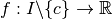 .
.
Un prolongement continu de
sur
est une fonction
qui est continue (y compris en
) et telle que pour tout
, on a
.
Exemple 2.5.4. La fonction de l’exemple 2.5.1 ne possède pas de prolongement continu. Par contre, la fonction de l’exemple 2.5.2 possède un prolongement continu dont le graphe est le suivant :
Dans le cas de cet exemple, puisque nous possédions déjà le graphe de la fonction, ce prolongement continu n’était pas très difficile à trouver.
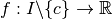 (où
(où  est un
intervalle et
est un
intervalle et 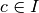 ) donnée, cette fonction admet un
prologement continu ? Intuitivement, il n’est pas très difficle de
répondre à cette question : il faut que la fonction
) donnée, cette fonction admet un
prologement continu ? Intuitivement, il n’est pas très difficle de
répondre à cette question : il faut que la fonction  se
rapproche d’une certaine valeur lorsqu’on se rapproche de
se
rapproche d’une certaine valeur lorsqu’on se rapproche de  ,
et ce de manière uniforme (il faut que la valeur de laquelle
,
et ce de manière uniforme (il faut que la valeur de laquelle  se rapproche par la gauche soit la même que celle de laquelle
se rapproche par la gauche soit la même que celle de laquelle
 se rapproche par la droite ). Néanmoins, cette réponse
intuitive soulève au moins trois questions.
se rapproche par la droite ). Néanmoins, cette réponse
intuitive soulève au moins trois questions.Que signifie rigoureusement que la fonction
 se rapproche
d’une valeur lorsqu’on se rapproche de
se rapproche
d’une valeur lorsqu’on se rapproche de  ?
?Comment savoir si la fonction
 se rapproche bien d’une
certaine valeur de manière uniforme et définitive lorsqu’on se
rapproche de
se rapproche bien d’une
certaine valeur de manière uniforme et définitive lorsqu’on se
rapproche de  ?
?Si
 se rapproche bien d’une certaine valeur de manière
uniforme et définitive lorsqu’on se rapproche de
se rapproche bien d’une certaine valeur de manière
uniforme et définitive lorsqu’on se rapproche de  , comment
calculer cette valeur ?
, comment
calculer cette valeur ?
Pour répondre à ces questions, nous avons besoin d’une nouvelle notion : celle de limite de fonction.
- 1
Remarque : pour la plupart des fonctions de référence, la démonstration n’est pas très compliquée. N’hésitez pas à essayer de faire vous-même la preuve par exemple pour une fonction constante ou pour la fonction identité.
- 2
La démonstration de ce théorème est en fait assez compliquée et nécessite de bien comprendre les propriétés fondamentales des nombres réels. Heureusement, son énoncé est très intuitif.
- 3
La démonstration de ce théorème est aussi assez compliquée.