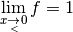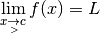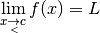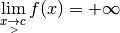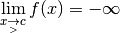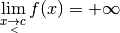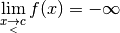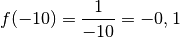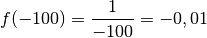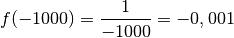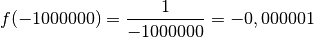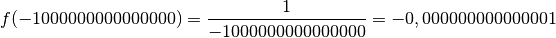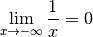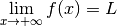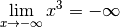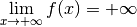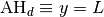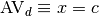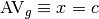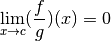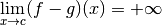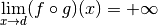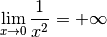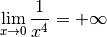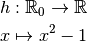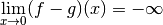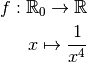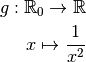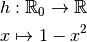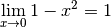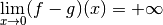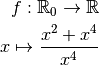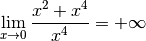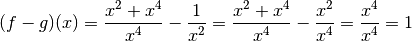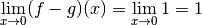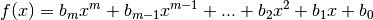3 Limites de fonctions¶
3.1 Définition et exemples¶
Pour découvrir la notion de limite qui est la formalisation de l’idée intuitive se rapprocher de (de façon définitive et uniforme) , commençons avec un exemple :
Définition 3.1.1. Soit la fonction

Son graphe est le suivant :
Au fur et à mesure que la variable  se rapproche de
se rapproche de  ,
de quelle valeur se rapproche
,
de quelle valeur se rapproche  ? Pour nous aider à y voir
plus clair, évaluons la fonction
? Pour nous aider à y voir
plus clair, évaluons la fonction  en plusieurs nombres qui se
rapprochent de
en plusieurs nombres qui se
rapprochent de  :
:
 se rapproche de
se rapproche de  , plus
, plus
 se rapproche de
se rapproche de  et ce de manière uniforme et
définitive : non seulement on se rapproche de cette valeur
et ce de manière uniforme et
définitive : non seulement on se rapproche de cette valeur  aussi bien par la droite que par la gauche , mais ce rapprochement se
fait autant que possible (sans pour autant que la fonction ne prenne
jamais la valeur
aussi bien par la droite que par la gauche , mais ce rapprochement se
fait autant que possible (sans pour autant que la fonction ne prenne
jamais la valeur  ) : les valeurs de
) : les valeurs de  se
rapprochent autant qu’on le souhaite de la valeur
se
rapprochent autant qu’on le souhaite de la valeur  à
condition que les valeurs de
à
condition que les valeurs de  soient assez proches de
soient assez proches de
 .
. se rapproche bien de
se rapproche bien de  quand les
quand les  se rapprochent de
se rapprochent de  : si on se fixe une
certaine marge d’erreur autour de
: si on se fixe une
certaine marge d’erreur autour de  (par exemple une marge
d’erreur de
(par exemple une marge
d’erreur de 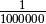 ), les valeurs de la fonction
), les valeurs de la fonction
 ne s’éloignent pas de
ne s’éloignent pas de  d’une distance supérieure
à l’erreur fixée à condition que les
d’une distance supérieure
à l’erreur fixée à condition que les  choisis soient assez
proches de
choisis soient assez
proches de  (avec une marge d’erreur de
(avec une marge d’erreur de
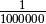 , les
, les  disponibles sont ceux ne
s’éloignant pas de
disponibles sont ceux ne
s’éloignant pas de  de plus de
de plus de  ).
Si la
fonction
).
Si la
fonction  se rapproche bien de
se rapproche bien de  quand les
quand les  se rapprochent de
se rapprochent de  , alors ce test devrait fonctionner quel
que soit la marge d’erreur (non nulle) qu’on s’est donnée, même si
celle-ci est extrêmement petite. Cette idée relativement naturelle
mais complexe est en fait la définition rigoureuse de la notion de
limite.
, alors ce test devrait fonctionner quel
que soit la marge d’erreur (non nulle) qu’on s’est donnée, même si
celle-ci est extrêmement petite. Cette idée relativement naturelle
mais complexe est en fait la définition rigoureuse de la notion de
limite.Définition 3.1.2. Soit un intervalle  éventuellement privé d’un point
éventuellement privé d’un point  . Soit
. Soit  .
.
On dit que
a une limite
en
si pour toute marge d’erreur
, il existe
tel que pour tout
qui est à une distance plus petite ou égale de
que
, c’est-à-dire tel que
, on a nécessairement que
est à une distance plus petite ou égale de
que
, c’est-à-dire qu’on a
. Dans ce cas, on note :
Exemple 3.1.3. La fonction

a comme limite  en
en  . On note :
. On note :
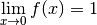
Remarque 3.1.4. Notons que dans l’exemple ci-dessus, la fonction  possède une
limite en
possède une
limite en  qui vaut
qui vaut  mais est également définie en
mais est également définie en
 de telle sorte que
de telle sorte que 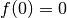 . Il est important de
comprendre qu’une limite d’une fonction en un point (si elle existe)
n’est pas toujours égale à la valeur de la fonction en ce point (la
fonction peut même ne pas être définie en ce point). C’est d’ailleurs
tout l’intérêt de la notion de limite : elle permet de parler d’une
valeur de laquelle se rapproche une fonction en un point sans que cette
fonction ne soit jamais égale à cette valeur.
. Il est important de
comprendre qu’une limite d’une fonction en un point (si elle existe)
n’est pas toujours égale à la valeur de la fonction en ce point (la
fonction peut même ne pas être définie en ce point). C’est d’ailleurs
tout l’intérêt de la notion de limite : elle permet de parler d’une
valeur de laquelle se rapproche une fonction en un point sans que cette
fonction ne soit jamais égale à cette valeur.
Voici à présent un théorème important mais que nous ne pourrons malheureusement pas démontrer :
Théorème 3.1.5. Soit un intervalle  éventuellement privé d’un point
éventuellement privé d’un point
 . Soit
. Soit  .
Si
.
Si  possède une limite en
possède une limite en  , alors cette limite est
unique.
, alors cette limite est
unique.
Il fait donc sens de parler de LA limite d’une fonction en un point. Ce théorème ne devrait pas vous surprendre : si on se rapproche de manière uniforme et définitive d’un endroit, on ne peut pas en même temps se rapprocher de manière uniforme et définitive d’un autre endroit.
Exemple 3.1.6. Soit la fonction carrée, dont le graphe est :
 et cette limite vaut
et cette limite vaut
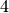 :
: 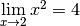 .
.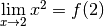 .
.Exemple 3.1.7. Soit la fonction dont le graphe est :
Cette fonction ne possède pas de limite en  : quand les
: quand les
 se rapprochent de
se rapprochent de  , les
, les  ne se
rapprochent pas uniformément d’un unique nombre (ils se rapproche de
ne se
rapprochent pas uniformément d’un unique nombre (ils se rapproche de
 par la gauche et de
par la gauche et de  par la droite ).
par la droite ).
Exemple 3.1.8. Soit la fonction dont le graphe est :
La fonction n’est pas définie en 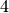 mais elle possède néanmoins
une limite en
mais elle possède néanmoins
une limite en 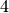 : quand les
: quand les  se rapprochent de
se rapprochent de
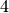 , les
, les  se rapprochent uniformément et
définitivement de
se rapprochent uniformément et
définitivement de 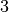 . On note :
. On note :

Définition 3.1.9. Soit la fonction dont le graphe est :
La fonction n’est pas définie en 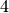 mais elle possède néanmoins
une limite en
mais elle possède néanmoins
une limite en 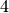 : quand les
: quand les  se rapprochent de
se rapprochent de
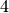 , les
, les  se rapprochent uniformément et
définitivement de
se rapprochent uniformément et
définitivement de  . On note :
. On note :

Exercice 3.1.10. À l’aide d’un graphique, déterminer si les limites suivantes existent. Si oui, donner les valeurs de celles-ci.




Exercice 3.1.11. Voici le graphe de la fonction  . Déterminer si les limites
suivantes existent. Si oui, donner les valeurs de celles-ci.
. Déterminer si les limites
suivantes existent. Si oui, donner les valeurs de celles-ci.

Exercice 3.1.12. Tracer le graphe d’une fonction  définie sur
définie sur
 qui n’a pas de limite en
qui n’a pas de limite en
 et qui a une limite en
et qui a une limite en  qui vaut
qui vaut 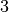 .
.
Solution.
Exercice 3.1.13. Déterminer si les limites suivantes si elles existent.










Exercice 3.1.14. Tracer le graphe d’une fonction  ayant les propriétés suivantes
:
ayant les propriétés suivantes
:
dom
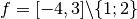
 est continue partout sauf en
est continue partout sauf en  .
. n’a pas de limite en
n’a pas de limite en  et en
et en 
 a une limite en
a une limite en  qui vaut
qui vaut  et une limite
en
et une limite
en  qui vaut
qui vaut 
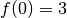 et
et 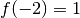
 a exactement deux racines et elles se trouvent entre
a exactement deux racines et elles se trouvent entre
 et
et  .
.
Solution.
3.2 Lien entre la continuité et les limites de fonctions¶
Dans la section précédente, nous avons pu observer que dans certains cas, la limite d’une fonction en un point où cette fonction est définie existe et est simplement égale à la valeur de la fonction en ce point. Dans tous les cas observés, la fonction était justement définie et continue en ce point. Il ne s’agit pas d’un hasard.
Théorème 3.2.1. Soit un intervalle  . Soit
. Soit  .
Soit
.
Soit 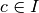 .
Alors
.
Alors  est continue en
est continue en  si et seulement si
si et seulement si  a une limite en
a une limite en  et
et 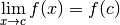 .
.
Malheureusement, la démonstration de ce théorème sort du cadre de ce cours.
Remarque 3.2.2. Il est vraiment dommage que nous ne puissions pas nous attarder sur la démonstration de ce théorème. En effet, celui-ci permet de relier la continuité aux limites, dont les définitions se ressemblent. Cette ressemblance n’est pas anodine : historiquement, ces deux notions ont été développées parallèlement et les mêmes idées ont été utilisées de part et d’autre pour arriver aux définitions actuelles.
Nous pouvons néanmoins expliquer brièvement la démonstration du théorème à partir de nos intuitions. Si une fonction est continue en un point, cela correspond au fait que son graphe ne possède pas de saut vertical en ce point, autrement dit que je peux approcher autant que je le souhaite la valeur de cette fonction en ce point à condition d’être assez proche de ce point. On retrouve assez directement l’intuition de limite : si les abscisses du graphe de la fonction se rapprochent du point considéré, les ordonnées se rapprochent donc nécessairement de l’image de ce point par la fonction, autrement dit la limite de la fonction en ce point est égale à l’image de la fonction en ce point. L’autre sens de la démonstration est tout aussi intuitif.
Avec ce théorème, nous pouvons calculer des limites de certaines fonctions sans pour autant pouvoir/devoir réaliser leurs graphes ! Donnons immédiatement un exemple.
Exemple 3.2.3. Soit la fonction
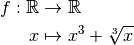
Supposons qu’on souhaite calculer la limite de cette fonction en
 . Cette fonction est continue car c’est la somme de deux
fonctions de référence (la fonction cubique et la fonction racine
cubique) qui sont continues. Par le théorème 3.2.1, puisque
. Cette fonction est continue car c’est la somme de deux
fonctions de référence (la fonction cubique et la fonction racine
cubique) qui sont continues. Par le théorème 3.2.1, puisque
 est bien définie et continue en
est bien définie et continue en  , on peut donc
affirmer que la limite
, on peut donc
affirmer que la limite 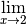 existe et vaut
existe et vaut
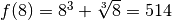 .
.
Exercice 3.2.4. Calculer les limites suivantes et justifier.




3.3 Lien entre les prolongements continus et les limites de fonctions¶
Dans la section précédente, nous avons vu que calculer la limite d’une fonction en un point où elle est définie et continue est on ne peut plus simple. Mais qu’en est-il si on veut calculer la limite d’une fonction en un point où elle n’est pas définie ? Commençons avec un exemple.
Exemple 3.3.1.
Considérons la fonction :
Cette fonction n’est pas définie en
mais on pourrait se demander si elle possède malgré tout une limite en
. Malheureusement, nous ne pouvons pas invoquer le théorème 3.2.1 pour cette éventuelle limite puisque bien que la fonction soit continue partout sur son domaine de définition, elle n’est pas définie en
. Si nous pouvions trouver un prolongement continu de cette fonction défini en
, nous pourrions aisément calculer cette limite en appliquant le théorème 3.2.1. En fait, l’existence de ce prolongement continu correspond précisément à l’existence de la limite que nous recherchons et la valeur de cet éventuel prolongement continu en
est précisément la valeur de la limite recherchée ? Dès lors, comment déterminer si la fonction
possède un prolongement continu en
? Pour ce faire, jouons un peu avec l’expression de
et simplifions. Pour tout
:
Pour tout
, nous avons donc
. Attention néanmoins : cette égalité est valable seulement si
. Elle n’a pas de sens si
.
Malgré cela, remarquons que l’expression
fait sens même si
:
. Autrement dit, si on pose :
La fonction
est définie partout même en
, est continue (y compris en
) et est telle que pour tout
:
. Il s’agit d’un prolongement continu de
!
Pour la fonction
, nous pouvons appliquer le théorème 3.2.1 :
. Or, comme pour tout
:
, on a donc :
En conclusion, la limite que nous recherchions existe et vaut
.
Dans l’exemple ci-dessus, nous avons relié l’existence d’une limite en un point où une fonction n’était pas définie à l’existence d’un prolongement continu de cette fonction en ce point. Nous avons vu qu’un tel prolongement continu existait et que sa valeur au point où la fonction initiale n’était pas définie correspondant précisément à la valeur recherchée. Ce n’est pas un hasard :
Théorème 3.3.2. Soit un intervalle  . Soit
. Soit 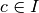 . Soit
. Soit 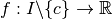 .
.
Alors
admet une limite en
si et seulement si
admet un prolongement continu en
. De plus, si la valeur de cette éventuelle limite est égale à l’image de cet éventuel prolongement continu en
.
Une fois de plus, nous ne pouvons malheureusement pas démontrer ce théorème dans ce cours. Mais à ce stade, celui-ci ne devrait pas vous surprendre. En effet, la notion de limite est précisément l’outil dont nous avions besoin pour répondre aux trois questions finales de la section 2.5. Grâce au théorème 3.3.2, nous pouvons à présent calculer des limites un peu moins triviales que celles que nous avons calculées dans la section précédente. En effet, lorsqu’on souhaite calculer la limite d’une fonction en un point où elle n’est pas défini, il suffit donc de rechercher un prolongement continu de cette fonction, ce qui peut se faire en manipulant et en simplifiant son expression.
Exercice 3.3.3. Les limites suivantes existent. Calculer celles-ci.








Remarque 3.3.4. Certaines personnes (pour être honnête : de nombreuses personnes) peu rigoureuses appliquent parfois la conclusion du théorème 3.2.1 même dans des cas où cette application n’est pas légitime, par exemple quand la fonction dont ils veulent calculer la limite n’est pas définie au point où ils veulent déterminer l’éventuelle limite. Pour donner un exemple précis, ces personnes écrivent :
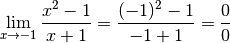
Ces personnes appellent alors ce genre de situation une indétermination .
Je vous interdis de faire de même dans ce cours.
Ce type de pratique est non rigoureuse et illogique (on applique un théorème alors que les hypothèses de ce théorème ne sont pas respectées), dangereuse (cela nuit à la compréhension de l’idée de limite (et d’infini) et fait écrire des suites de symboles qui n’ont pas de sens) et inutile (de nombreux mathématiciens dans le monde calculent des limites très efficacement sans avoir besoin d’écrire de telles horreurs). Plutôt que de ne pas réfléchir et d’écrire de façon automatique des choses qui n’ont pas de sens, prenez toujours le temps de vérifier si les hypothèses des résultats que vous souhaitez invoquer sont vérifiées et d’être certain de comprendre ce que vous êtes en train de faire.
3.4 Divergence de fonctions en un point¶
Exemple 3.4.1. Considérons la fonction :
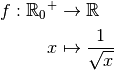
dont voici le graphe :
Que se passe-t-il quand les  se rapprochent de
se rapprochent de  ? Les
? Les
 ne se rapprochent certainement pas d’un nombre réel ! Si on
teste avec certaines valeurs de
ne se rapprochent certainement pas d’un nombre réel ! Si on
teste avec certaines valeurs de  qui se rapprochent de
qui se rapprochent de
 , on constate immédiatement que les
, on constate immédiatement que les  deviennent de
plus en plus grands :
deviennent de
plus en plus grands :
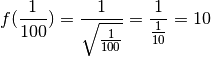

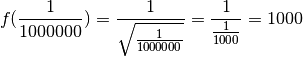
On remarque même qu’à condition de se rapprocher suffisament de
 , les valeurs de la fonction deviendront aussi grandes que l’on
veut. Autrement dit, on peut se donner n’importe quelle borne
supérieure, les valeurs
, les valeurs de la fonction deviendront aussi grandes que l’on
veut. Autrement dit, on peut se donner n’importe quelle borne
supérieure, les valeurs  de cette fonction dépassent par le
haut cette borne supérieure de façon uniforme et définitive à condition
de choisir des
de cette fonction dépassent par le
haut cette borne supérieure de façon uniforme et définitive à condition
de choisir des  suffisament proche de
suffisament proche de  . Ce
comportement est appelé divergence (vers
. Ce
comportement est appelé divergence (vers  ) et nous venons
d’en donner la définition intuitive.
) et nous venons
d’en donner la définition intuitive.
Donnons à présent la définition rigoureuse de divergence (vers
 ).
).
Définition 3.4.2. Soit un intervalle  éventuellement privé d’un point
éventuellement privé d’un point  . Soit
. Soit  .
.
On dit que
diverge (vers
) en
si pour toute borne supérieure
, il existe
tel que pour tout
qui est à une distance plus petite ou égale de
que
, c’est-à-dire tel que
, on a nécessairement que
est plus grand ou égal à
, c’est-à-dire que
. Dans ce cas, on note :
Remarque 3.4.3. Attention : cette remarque est extrêmement importante.
Lorsqu’une fonction diverge (vers
) en un point, elle n’a pas de limite en ce point. Diverger vers
ne signifie pas se rapprocher d’un nombre appelé
(
n’est pas un nombre réel). On utilise pourtant la même notation pour parler de limite et de divergence : cela est extrêmement malheureux et absolument pas pédagogique. Cette notation étant néanmoins utilisée par tous, nous l’utiliserons également.
 ne se
lit pas la fonction
ne se
lit pas la fonction  a comme limite/converge vers
a comme limite/converge vers
 en
en  mais bien la fonction
mais bien la fonction  diverge
vers
diverge
vers  en
en  . La convergence (avoir une limite)
et la divergence sont deux notions complétement différentes.
. La convergence (avoir une limite)
et la divergence sont deux notions complétement différentes.Exemple 3.4.4. La fonction
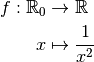
dont le graphe est :
diverge vers  en
en  . On note :
. On note :
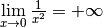 .
.
Il existe un autre phénomène possible lorsqu’une fonction ne converge
pas en un point, très semblable à la divergence vers  :
il s’agit de la divergence vers
:
il s’agit de la divergence vers  . Pour l’introduire,
commençons avec un exemple.
. Pour l’introduire,
commençons avec un exemple.
Exemple 3.4.5. Considérons la fonction

dont le graphe est :
Que se passe-t-il quand les  se rapprochent de
se rapprochent de  ? À
nouveau, les
? À
nouveau, les  ne se rapprochent certainement pas d’un nombre
réel ! Si on teste avec certaines valeurs de
ne se rapprochent certainement pas d’un nombre
réel ! Si on teste avec certaines valeurs de  qui se
rapprochent de
qui se
rapprochent de  , on constate immédiatement que les
, on constate immédiatement que les  deviennent de plus en plus grands négativement :
deviennent de plus en plus grands négativement :
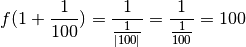





On remarque même qu’à condition de se rapprocher suffisament de
 , les valeurs de la fonction deviendront aussi grandes
négativement que l’on veut. Autrement dit, on peut se donner n’importe
quelle borne inférieure, les valeurs
, les valeurs de la fonction deviendront aussi grandes
négativement que l’on veut. Autrement dit, on peut se donner n’importe
quelle borne inférieure, les valeurs  de cette fonction
dépassent par le bas cette borne supérieure de façon uniforme et
définitive à condition de choisir des
de cette fonction
dépassent par le bas cette borne supérieure de façon uniforme et
définitive à condition de choisir des  suffisament proche de
suffisament proche de
 . Ce comportement est appelé divergence (vers
. Ce comportement est appelé divergence (vers  )
et nous venons d’en donner la définition intuitive.
)
et nous venons d’en donner la définition intuitive.
Donnons à présent la définition rigoureuse de divergence (vers
 ).
).
Définition 3.4.6. Soit un intervalle  éventuellement privé d’un point
éventuellement privé d’un point  . Soit
. Soit  .
.
On dit que
diverge (vers
) en
si pour toute borne supérieure
, il existe
tel que pour tout
qui est à une distance plus petite ou égale de
que
, c’est-à-dire tel que
, on a nécessairement que
est plus grand ou égal à
, c’est-à-dire tel que
. Dans ce cas, on note :
Remarque 3.4.7. Même remarque que pour la divergence vers  : diverger
vers
: diverger
vers  ne signifie pas avoir comme limite un nombre
appelé
ne signifie pas avoir comme limite un nombre
appelé  .
.
Exemple 3.4.8. La fonction

dont le graphe est :
diverge vers  en
en  . On note :
. On note :
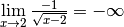 .
.
 et divergence
et divergence sont mutuellement exclusives. En effet :
sont mutuellement exclusives. En effet :- Si une fonction converge (a une limite) en un point, ses valeurs ne peuvent pas devenir arbitrairement grandes (que ce soit positivement ou négativement) puisque qu’elle se rapproche de la limite (qui est un nombre réel).
Si une fonction diverge vers
 en un point, ses valeurs
ne peuvent se rapprocher d’un nombre réel (puisque celles-ci
deviennent de plus en plus grandes positivement au fur et à mesure
qu’on se rapproche du point où la fonction diverge) et ne peuvent
devenir arbitrairement grandes négativement (puisque celles-ci
deviennent de plus en plus grandes positivement au fur et à
mesure qu’on se rapproche du point où la fonction diverge).
en un point, ses valeurs
ne peuvent se rapprocher d’un nombre réel (puisque celles-ci
deviennent de plus en plus grandes positivement au fur et à mesure
qu’on se rapproche du point où la fonction diverge) et ne peuvent
devenir arbitrairement grandes négativement (puisque celles-ci
deviennent de plus en plus grandes positivement au fur et à
mesure qu’on se rapproche du point où la fonction diverge).Si une fonction diverge vers
 en un point, ses valeurs
ne peuvent se rapprocher d’un nombre réel (puisque celles-ci
deviennent de plus en plus grandes négativement au fur et à mesure
qu’on se rapproche du point où la fonction diverge) et ne peuvent
devenir arbitrairement grandes négativement (puisque celles-ci
deviennent de plus en plus grandes négativement au fur et à
mesure qu’on se rapproche du point où la fonction diverge).
en un point, ses valeurs
ne peuvent se rapprocher d’un nombre réel (puisque celles-ci
deviennent de plus en plus grandes négativement au fur et à mesure
qu’on se rapproche du point où la fonction diverge) et ne peuvent
devenir arbitrairement grandes négativement (puisque celles-ci
deviennent de plus en plus grandes négativement au fur et à
mesure qu’on se rapproche du point où la fonction diverge).
Proposition 3.4.9. Soit un intervalle  éventuellement privé d’un point
éventuellement privé d’un point  . Soit
. Soit  .
.
Si
 possède une limite en
possède une limite en  , alors
, alors  ne
diverge pas vers
ne
diverge pas vers  en
en  et ne diverge pas vers
et ne diverge pas vers
 en
en  .
.Si
 diverge vers
diverge vers  en
en  , alors
, alors
 ne possède pas une limite en
ne possède pas une limite en  et ne diverge pas
vers
et ne diverge pas
vers  en
en  .
.Si
 diverge vers
diverge vers  en
en  , alors
, alors
 ne possède pas une limite en
ne possède pas une limite en  et ne diverge pas
vers
et ne diverge pas
vers  en
en  .
.
 et de
divergence vers
et de
divergence vers  , donnons quelques exemples et
contre-exemples supplémentaires.
, donnons quelques exemples et
contre-exemples supplémentaires.Contre-exemple 3.4.10. Les seules fonctions de référence qui ne sont pas définies sur tout  sont la fonction racine carrée et la fonction
inverse. Nous savons déjà que la fonction racine carrée a comme limite
sont la fonction racine carrée et la fonction
inverse. Nous savons déjà que la fonction racine carrée a comme limite
 lorsque
lorsque  tend vers
tend vers  , mais qu’en est-il de
la fonction inverse ? Diverge-t-elle ?
Rappelons que la fonction inverse est la fonction :
, mais qu’en est-il de
la fonction inverse ? Diverge-t-elle ?
Rappelons que la fonction inverse est la fonction :
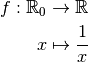
Son graphe est le suivant.
Lorsque les 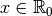 se rapprochent de
se rapprochent de  ,
les nombres
,
les nombres 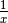 ne se rapprochent certainement pas d’un
nombre de manière uniforme et définitive. Mais ils ne deviennent pas non
plus arbitrairement grands positivement de manière uniforme et
définitive (ils le deviennt à droite de
ne se rapprochent certainement pas d’un
nombre de manière uniforme et définitive. Mais ils ne deviennent pas non
plus arbitrairement grands positivement de manière uniforme et
définitive (ils le deviennt à droite de  , mais pas à gauche )
et ils ne deviennent pas non plus arbitrairement grands négativement de
manière uniforme et définitive (ils le deviennt à gauche de
, mais pas à gauche )
et ils ne deviennent pas non plus arbitrairement grands négativement de
manière uniforme et définitive (ils le deviennt à gauche de  ,
mais pas à droite ). En conclusion, la fonction inverse n’a pas de
limite en
,
mais pas à droite ). En conclusion, la fonction inverse n’a pas de
limite en  , mais ne diverge pas non plus en
, mais ne diverge pas non plus en  (que ce
soit vers
(que ce
soit vers  ou vers
ou vers  ).
).
Remarque 3.4.11. La fonction inverse ne diverge pas vers  ou vers
ou vers
 en
en  , mais par contre son produit avec elle-même
diverge vers
, mais par contre son produit avec elle-même
diverge vers  en
en  : voir exemple
3.4.4.
: voir exemple
3.4.4.
Exemple 3.4.12. La fonction 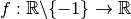 dont
le graphe est le suivant :
dont
le graphe est le suivant :
diverge vers  en
en  . On note :
. On note :
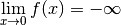 .
.
Exemple 3.4.13. La fonction  dont le graphe est le
suivant :
dont le graphe est le
suivant :
diverge vers  en
en  (même si la fonction est
définie en
(même si la fonction est
définie en  de telle sorte que
de telle sorte que  ). On note :
). On note :
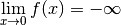 .
.
Contre-exemple 3.4.14. La fonction  dont le graphe est le
suivant :
dont le graphe est le
suivant :
ne converge pas et ne diverge pas en  .
.
Contre-exemple 3.4.15. La fonction  dont
le graphe est le suivant :
dont
le graphe est le suivant :
ne converge pas et ne diverge pas en  .
.
À présent, exerçons-nous un peu.
Exercice 3.4.16. À l’aide d’un graphique, déterminer si les fonctions divergent au point
considéré. Si oui, donner le type de divergence (vers  ou
vers
ou
vers  ).
).




Exercice 3.4.17. Voici le graphe d’une fonction réelle  . Déterminer l’ensemble
des points où elle diverge.
. Déterminer l’ensemble
des points où elle diverge.

Exercice 3.4.18. Tracer le graphe d’une fonction  définie sur
définie sur
 qui diverge vers
qui diverge vers  en
en  et qui ne diverge et ne converge pas en
et qui ne diverge et ne converge pas en  .
.
Solution.
Exercice 3.4.19. Déterminer si les fonctions dont les graphes sont donnés ci-dessous divergent aux points indiqués.
Solution.
|
|
Exercice 3.4.20 Tracer le graphe d’une fonction  ayant les propriétés suivantes
:
ayant les propriétés suivantes
:
Solution.
Exercice 3.4.21 Tracer le graphe d’une fonction
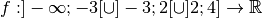 qui est
continue partout sauf en
qui est
continue partout sauf en  et
et  , qui a comme limite
, qui a comme limite
 en
en  et comme limite
et comme limite  en
en
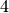 , qui n’a pas de limite en
, qui n’a pas de limite en  , qui diverge vers
, qui diverge vers
 en -3 et qui ne diverge pas en
en -3 et qui ne diverge pas en  .
.
Solution.
Exercice 3.4.22 Déterminer si les fonctions convergent ou divergent au point considéré.
Si elles convergent, donner la limite. Si elles divergent, donner le
type de divergence (vers  ou vers
ou vers  ).
).








3.5 Limites à gauche et limites à droite¶
Exemple 3.5.1. La fonction  dont le graphe est :
dont le graphe est :
 . Lorsque les abscisses se rapprochent
de
. Lorsque les abscisses se rapprochent
de  , les points du graphe de
, les points du graphe de  ne se rapprochent pas
définitivement et uniformément d’une seule valeur.
ne se rapprochent pas
définitivement et uniformément d’une seule valeur. , la fonction réduite
, la fonction réduite
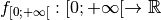 possède bien une
limite en
possède bien une
limite en  :
:On a : 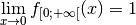 . De même,
si nous ne considérons que les points du graphe dont les abscisses sont
inférieures à
. De même,
si nous ne considérons que les points du graphe dont les abscisses sont
inférieures à  , la fonction réduite
, la fonction réduite
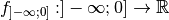 possède bien une
limite en
possède bien une
limite en  :
:
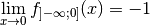 .
.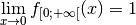 ,
cela signifie précisément que la fonction
,
cela signifie précisément que la fonction  possède une limite
à droite de 0 et que celle-ci vaut
possède une limite
à droite de 0 et que celle-ci vaut  , ce qu’on note :
, ce qu’on note :
Lorsqu’on affirme que
, cela signifie précisément que la fonction
possède une limite à gauche de 0 et que celle-ci vaut
, ce qu’on note :
Donnons à présent la définition générale de limite à droite et de limite à gauche : il s’agit simplement d’utiliser la définition de limite et de restriction de fonction.
Définition 3.5.2. Soit un intervalle  éventuellement privé d’un point
éventuellement privé d’un point  . Soit
. Soit  .
.
On dit que
a une limite à droite
en
si la fonction
a comme limite
en
. On note :
On dit que
a une limite à gauche
en
si la fonction
a comme limite
en
. On note :
Remarque 3.5.3. Certaines personnes préfèrent utiliser les notations
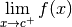 pour les limites à droite et
pour les limites à droite et
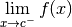 pour les limites à gauche. Je
vous déconseille d’utiliser ces notations.
pour les limites à gauche. Je
vous déconseille d’utiliser ces notations.
Donnons quelques exemples et contre-exemples.
Exemple 3.5.4. La fonction  dont le graphe est :
dont le graphe est :
 qui vaut
qui vaut  :
:
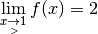 .
. .
.Exemple 3.5.5. La fonction carrée  dont le graphe
est :
dont le graphe
est :
 qui vaut
qui vaut 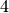 :
:
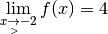 .
. a aussi une limite à gauche en
a aussi une limite à gauche en  qui
vaut aussi
qui
vaut aussi 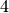 :
:
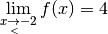 .
.Contre-exemple 3.5.6. La fonction inverse  dont le graphe
est :
dont le graphe
est :
n’a pas de limite à droite en  et n’a pas de limite à gauche en
et n’a pas de limite à gauche en
 .
.
Dans tous les exemples déjà rencontrés, remarquons que le seul où la fonction admet une limite à droite et une limite à gauche au point considéré et que ces deux limites sont égales correspond au cas où la fonction admet une (véritable) limite en ce point, qui est d’ailleurs égale à l’unique valeur de la limite à droite et de la limite à gauche.
Ce n’est pas un hasard : pour avoir une limite en un point  ,
une fonction
,
une fonction  doit se rapprocher de façon définitive et
uniforme d’une unique valeur, elle doit donc avoir une limite à gauche
en ce point et une limite à droite en ce point et celles-ci doivent être
identiques. L’inverse est vrai aussi : si une fonction
doit se rapprocher de façon définitive et
uniforme d’une unique valeur, elle doit donc avoir une limite à gauche
en ce point et une limite à droite en ce point et celles-ci doivent être
identiques. L’inverse est vrai aussi : si une fonction  a une
limite à gauche en un point
a une
limite à gauche en un point  et une limite à droite en
et une limite à droite en
 et que celles-ci sont égales, alors
et que celles-ci sont égales, alors  se rapprochent
bien définitivement et uniformément de cet unique nombre au fur et à
mesure qu’on se rapproche de
se rapprochent
bien définitivement et uniformément de cet unique nombre au fur et à
mesure qu’on se rapproche de  ! Plus rigoureusement, on peut
démontrer :
! Plus rigoureusement, on peut
démontrer :
Proposition 3.5.7. Soit un intervalle  éventuellement privé d’un point
éventuellement privé d’un point  . Soit
. Soit  .
.
Alors
possède une limite
en
si et seulement si
possède une limite à droite
en
et une limite à gauche
en
et que celles-ci sont égales :
.
Remarque 3.5.8. Certaines personnes aiment beaucoup les limites à droite et les limites à gauche, à tel point qu’elles définissent celles-ci en premier et les utilisent pour définir la notion de limite générale.
Pourtant, c’est bien la notion de limite qui est fondamentale, si utile et qui permet de démontrer d’impressionnants résultats mathématiques. De plus, les notions de limite à droite et limite à gauche ne se généralisent pas lorsqu’on ne peut pas parler de droite et de gauche tandis que la notion de limite plus gobale se généralise dans de nombreux contextes.
Pour ces raisons, nous n’insisterons volontairement pas sur les notions de limites à droite et de limite à gauche dans ce cours.
Exemple 3.5.9. Considérons la fonction inverse
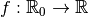 dont le graphe est :
dont le graphe est :
Comme nous l’avons vu dans la section précédente, cette fonction ne
diverge pas (que ce soit vers  ou
ou  en
en
 ). Par contre, si nous ne considérons que les points de son
domaine qui sont plus grands ou égaux à
). Par contre, si nous ne considérons que les points de son
domaine qui sont plus grands ou égaux à  , on obtient la
fonction
, on obtient la
fonction 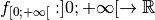 dont le
graphe est :
dont le
graphe est :
 en
en  :
:
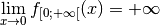 .
. , on obtient
la fonction
, on obtient
la fonction
 dont
le graphe est :
dont
le graphe est : en
en  :
:
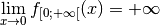 .
. diverge vers
diverge vers  à droite de
à droite de
 , ce qu’on note
, ce qu’on note
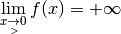 et qu’elle
diverge vers
et qu’elle
diverge vers  à gauche de
à gauche de  , ce qu’on note
, ce qu’on note
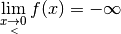 .
.Définition 3.5.10. Soit un intervalle  éventuellement privé d’un point
éventuellement privé d’un point  . Soit
. Soit  .
.
On dit que
diverge vers :math:`+infty` à droite en
si la fonction
diverge vers
en
. On note :
On dit que
diverge vers :math:`-infty` à droite en
si la fonction
diverge vers
en
. On note :
On dit que
a diverge vers :math:`+infty` à gauche en
si la fonction
diverge vers
en
. On note :
On dit que
a diverge vers :math:`-infty` à gauche en
si la fonction
diverge vers
en
. On note :
On a un résultat équivalent pour les divergence à gauche et à droite à celui qu’on avait pour les limites :
Proposition 3.5.11. Soit un intervalle  éventuellement privé d’un point
éventuellement privé d’un point  . Soit
. Soit  .
.
Alors
diverge vers
en
si et seulement si
diverge vers
à droite en
et
diverge vers
à gauche en
.
De plus,
diverge vers
en
si et seulement si
diverge vers
à droite en
et
diverge vers
à gauche en
.
Exemple 3.5.12. La fonction  dont le graphe est :
dont le graphe est :
diverge vers  à droite en
à droite en  et diverge vers
et diverge vers
 à gauche en
à gauche en  . Elle diverge vers
. Elle diverge vers  en
en  .
.
Exemple 3.5.13. La fonction  dont le graphe est :
dont le graphe est :
diverge vers  à gauche en
à gauche en  . Elle ne diverge pas
à droite en
. Elle ne diverge pas
à droite en  .
.
Exemple 3.5.14. La fonction carrée  dont le graphe
est :
dont le graphe
est :
ne diverge ni à gauche ni à droite en  .
.
Exercice 3.5.15. Pour la fonction dont le graphe est ci-dessous, quels sont les points où la fonction a une limite à gauche ou à droite mais n’a pas de limite ? Quels sont les points où la fonction diverge à gauche ou à droite mais ne diverge pas ? Pour tous ces points, donner les limites ou les divergences à gauche ou à droite éventuelles.
Solution. Le seul point où la fonction n’a pas de limite ou ne diverge pas est
 . La fonction a une limite à gauche en
. La fonction a une limite à gauche en  qui vaut
qui vaut
 et diverge vers
et diverge vers  à droite en
à droite en  .
.
Exercice 3.5.16. Tracer le graphe d’une fonction  ayant les propriétés suivantes
:
ayant les propriétés suivantes
:
Solution.
Exemple 3.5.17. Déterminer quelles sont les limites et les divergence à gauche et à droite.





Exercice 3.5.18. Tracer le graphe d’une fonction
 qui est
continue partout sauf en
qui est
continue partout sauf en  et
et  , qui vaut
, qui vaut  en
en
 ,
, 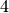 en
en  et
et 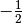 en
en 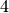 ,
qui a comme limite à gauche
,
qui a comme limite à gauche  en
en  et comme limite à
droite
et comme limite à
droite  en
en  , qui a comme limite à gauche
, qui a comme limite à gauche  en
en  et qui diverge vers
et qui diverge vers  à droite en
à droite en  ,
qui diverge vers
,
qui diverge vers  à gauche en
à gauche en  et qui diverge
vers
et qui diverge
vers  à droite en
à droite en  .
.
Solution.
Exercice 3.5.19. Déterminer si les fonctions convergent ou divergent à droite ou à gauche
au point considéré. Si elles convergent à droite ou à gauche, donner la
limite à droite ou à gauche. Si elles divergent à droite ou à gauche,
donner le type de divergence (vers  ou vers
ou vers
 ). N’hésitez pas à vous aider d’un graphe.
). N’hésitez pas à vous aider d’un graphe.





3.6 Limites et divergence de fonctions en  et
et  ¶
¶
 en un point
en un point
 . Mais l’idée de limite (et de divergence)
peut également être déclinée pour parler du comportement
asymptotique d’une fonction, c’est-à-dire du comportement des
nombres
. Mais l’idée de limite (et de divergence)
peut également être déclinée pour parler du comportement
asymptotique d’une fonction, c’est-à-dire du comportement des
nombres  pour des valeurs de l’argument
pour des valeurs de l’argument  qui
deviennt de plus en plus grandes ou de plus en plus petites (grandes
négativement).
qui
deviennt de plus en plus grandes ou de plus en plus petites (grandes
négativement).Exemple 3.6.1. Nous souhaiterions pouvoir parler du comportement asymptotique de la fonction inverse, dont le graphe est pour rappel le suivant.
Nous aimerions savoir ce que deviennent les nombres  au fur
et à mesure que nous considérons des
au fur
et à mesure que nous considérons des  de plus en plus grands.
Voyons d’abord ce que vaut
de plus en plus grands.
Voyons d’abord ce que vaut  pour certaines valeurs de
pour certaines valeurs de
 particulières qui sont de plus en plus grandes :
particulières qui sont de plus en plus grandes :
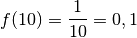

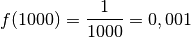
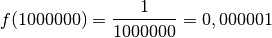
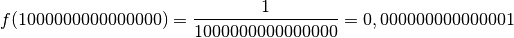
 par des nombres positifs
arbitrairement grands, le résultat sera un nombre positif
arbitrairement proche de
par des nombres positifs
arbitrairement grands, le résultat sera un nombre positif
arbitrairement proche de  . Au fur à mesure que les abscisses
. Au fur à mesure que les abscisses
 des points du graphes grandissent, les ordonnées
des points du graphes grandissent, les ordonnées
 associées se rapprochent uniformément et définitivement
de
associées se rapprochent uniformément et définitivement
de  . Nous retrouvons l’idée de limite : la nouveauté étant
que nous observons le comportement de la fonction non pas à l’approche
d’un point, mais son comportement pour des nombres de plus en plus
grands.
. Nous retrouvons l’idée de limite : la nouveauté étant
que nous observons le comportement de la fonction non pas à l’approche
d’un point, mais son comportement pour des nombres de plus en plus
grands. quand
quand  tend vers
tend vers  . On note :
. On note : qui sont de plus en plus petites :
qui sont de plus en plus petites :
Plus généralement, si nous divisons
par des nombres négatifs arbitrairement petits, le résultat sera un nombre négatif arbitrairement proche de
. Au fur à mesure que les abscisses
des points du graphes diminuent, les ordonnées
associées se rapprochent uniformément et définitivement de
. Nous retrouvons une fois de plus l’idée de limite : la nouveauté étant que nous observons le comportement de la fonction non pas à l’approche d’un point, mais son comportement pour des nombres de plus en plus petits.
 quand
quand  tend vers
tend vers  . On note :
. On note :Remarque 3.6.2. Il se trouve que la fonction inverse a la même limite pour  tendant vers
tendant vers  et pour
et pour  tendant vers
tendant vers
 . Ce n’est bien évidemment pas toujours le cas. Par
exemple, la fonction dont le graphe est ci-dessous a comme limite
. Ce n’est bien évidemment pas toujours le cas. Par
exemple, la fonction dont le graphe est ci-dessous a comme limite
 pour
pour  tendant vers
tendant vers  et
et  pour
pour
 tendant vers
tendant vers  .
.
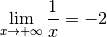
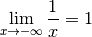
Donnons les définitions de limite d’une fonction pour  qui tend
vers
qui tend
vers  ou vers
ou vers  . Celle-ci est très
similaire à la définition de limite d’une fonction en un point et est
construite de la même manière.
. Celle-ci est très
similaire à la définition de limite d’une fonction en un point et est
construite de la même manière.
Définition 3.6.3. Soit un intervalle  non majoré. Soit
non majoré. Soit  .
.
On dit que
a une limite
pour
qui tend vers
si pour toute marge d’erreur
, il existe
tel que pour tout
qui est plus grand ou égal à
, c’est-à-dire tel que
, on a nécessairement que
est à une distance plus petite ou égale de
que
, c’est-à-dire qu’on a
. Dans ce cas, on note :
Définition 3.6.4. Soit un intervalle  non minoré. Soit
non minoré. Soit  .
.
On dit que
a une limite
pour
qui tend vers
si pour toute marge d’erreur
, il existe
tel que pour tout
qui est plus petit ou égal à
, c’est-à-dire tel que
, on a nécessairement que
est à une distance plus petite ou égale de
que
, c’est-à-dire qu’on a
. Dans ce cas, on note :
Donnons quelques exemples et contre-exemples.
Exemple 3.6.5. La fonction dont le graphe est donné ci-dessous a comme limite 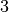 pour
pour  qui tend vers
qui tend vers  .
.
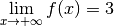
Pour cette fonction, il ne fait pas sens de parler d’une éventuelle
limite pour  qui tend vers
qui tend vers  puisque son domaine
de définition est
puisque son domaine
de définition est 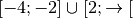 .
.
Exemple 3.6.6. La fonction dont le graphe est donné ci-dessous a comme limite
 pour
pour  qui tend vers
qui tend vers  et pour
et pour
 qui tend vers
qui tend vers  .
.
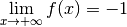
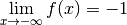
Contre-exemple 3.6.7. La fonction dont le graphe est donné ci-dessous n’a pas de limite pour
 qui tend vers
qui tend vers  et n’a pas de limite pour
et n’a pas de limite pour
 qui tend vers
qui tend vers  .
.
En effet, peu importe si on considère des nombres  de plus en
plus grands ou de plus en plus petits, les nombres
de plus en
plus grands ou de plus en plus petits, les nombres  associées ne finiront jamais par se rapprocher de manière uniforme et
définitive d’une valeur unique. Ils continueront d’osciller autour de
associées ne finiront jamais par se rapprocher de manière uniforme et
définitive d’une valeur unique. Ils continueront d’osciller autour de
 encore et encore.
encore et encore.
Contre-exemple 3.6.8. La fonction dont le graphe est donné ci-dessous n’a pas de limite pour
 qui tend vers
qui tend vers  mais a comme limite
mais a comme limite  pour
pour  qui tend vers
qui tend vers  .
.

 qui tend vers
qui tend vers  ou pour
ou pour  qui tend
vers
qui tend
vers  , on peut parler de la divergence vers
, on peut parler de la divergence vers
 ou vers
ou vers  pour
pour  qui tend vers
qui tend vers
 ou pour
ou pour  qui tend vers
qui tend vers  . Une
fois de plus, introduisons cette nouvelle notion avec un exemple.
. Une
fois de plus, introduisons cette nouvelle notion avec un exemple.Exemple 3.6.9. Nous souhaiterions pouvoir parler du comportement asymptotique de la fonction cubique, dont le graphe est pour rappel le suivant.
Nous aimerions savoir ce que deviennent les nombres  au fur
et à mesure que nous considérons des
au fur
et à mesure que nous considérons des  de plus en plus grands.
Voyons d’abord ce que vaut
de plus en plus grands.
Voyons d’abord ce que vaut  pour certaines valeurs de
pour certaines valeurs de
 particulières qui sont de plus en plus grandes :
particulières qui sont de plus en plus grandes :
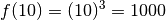
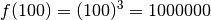
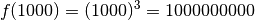

 des
points du graphes grandissent, les ordonnées
des
points du graphes grandissent, les ordonnées  deviennent
uniformément et définitivement aussi grandes que l’on veut. Nous
retrouvons l’idée de divergence : la nouveauté étant que nous
observons le comportement de la fonction non pas à l’approche d’un
point, mais son comportement pour des nombres de plus en plus grands.
deviennent
uniformément et définitivement aussi grandes que l’on veut. Nous
retrouvons l’idée de divergence : la nouveauté étant que nous
observons le comportement de la fonction non pas à l’approche d’un
point, mais son comportement pour des nombres de plus en plus grands. quand
quand  tend vers
tend vers  . On note :
. On note : qui sont de plus en plus petites :
qui sont de plus en plus petites :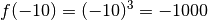
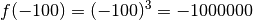
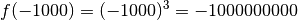

 des
points du graphes diminuent, les ordonnées
des
points du graphes diminuent, les ordonnées  associées
deviennent uniformément et définitivement aussi petites que l’on veut.
Nous retrouvons une fois de plus l’idée de divergence : la nouveauté
étant que nous observons le comportement de la fonction non pas à
l’approche d’un point, mais son comportement pour des nombres de plus
en plus petits.
associées
deviennent uniformément et définitivement aussi petites que l’on veut.
Nous retrouvons une fois de plus l’idée de divergence : la nouveauté
étant que nous observons le comportement de la fonction non pas à
l’approche d’un point, mais son comportement pour des nombres de plus
en plus petits. quand
quand  tend vers
tend vers  . On note :
. On note : ou vers
ou vers
 d’une fonction pour
d’une fonction pour  qui tend vers
qui tend vers
 ou vers
ou vers  . Celle-ci est très similaire à
la définition de divergence d’une fonction en un point et est
construite de la même manière.
. Celle-ci est très similaire à
la définition de divergence d’une fonction en un point et est
construite de la même manière.Définition 3.6.10. Soit un intervalle  non majoré. Soit
non majoré. Soit  .
.
On dit que
a diverge vers
pour
qui tend vers
si pour toute borne supérieure
, il existe
tel que pour tout
qui est plus grand ou égal à
, c’est-à-dire tel que
, on a nécessairement que
est plus grand ou égal à
, c’est-à-dire qu’on a
. Dans ce cas, on note :
Définition 3.6.11. Soit un intervalle  non majoré. Soit
non majoré. Soit  .
.
On dit que
a diverge vers
pour
qui tend vers
si pour toute borne inférieure
, il existe
tel que pour tout
qui est plus grand ou égal à
, c’est-à-dire tel que
, on a nécessairement que
est plus petit ou égal à
, c’est-à-dire qu’on a
. Dans ce cas, on note :
Définition 3.6.12. Soit un intervalle  non minoré. Soit
non minoré. Soit  .
.
On dit que
a diverge vers
pour
qui tend vers
si pour toute borne supérieure
, il existe
tel que pour tout
qui est plus petit ou égal à
, c’est-à-dire tel que
, on a nécessairement que
est plus grand ou égal à
, c’est-à-dire qu’on a
. Dans ce cas, on note :
Définition 3.6.13. Soit un intervalle  non majoré. Soit
non majoré. Soit  .
.
On dit que
a diverge vers
pour
qui tend vers
si pour toute borne inférieure
, il existe
tel que pour tout
qui est plus grand ou égal à
, c’est-à-dire tel que
, on a nécessairement que
est plus petit ou égal à
, c’est-à-dire qu’on a
. Dans ce cas, on note :
Donnons quelques exemples et contre-exemples.
Exemple 3.6.14. La fonction valeur absolue diverge vers  pour
pour  qui tend vers
qui tend vers  et diverge ves
et diverge ves  pour
pour
 qui tend vers
qui tend vers  .
.
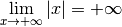
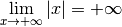
Exemple 3.6.15. La fonction racine carrée diverge vers  pour
pour  qui tend vers
qui tend vers  . Il ne fait pas sens de parler d’une
limite ou de divergence pour
. Il ne fait pas sens de parler d’une
limite ou de divergence pour  qui tend vers
qui tend vers  pour la racine carrée puisqu’elle n’est pas définie sur l’ensemble des
réels strictement négatifs.
pour la racine carrée puisqu’elle n’est pas définie sur l’ensemble des
réels strictement négatifs.

Exemple 3.6.16. La fonction dont le graphe est donné ci-dessous diverge vers
 pour
pour  qui tend vers
qui tend vers  et diverge
vers
et diverge
vers  pour
pour  qui tend vers
qui tend vers  .
.
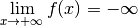
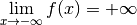
Contre-exemple 3.6.17. La fonction dont le graphe est donné ci-dessous ne diverge pas pour
 qui tend vers
qui tend vers  et ne diverge pas pour
et ne diverge pas pour  qui tend vers
qui tend vers  .
.
Contre-exemple 3.6.18. La fonction dont le graphe est donné ci-dessous diverge vers
 pour
pour  qui tend vers
qui tend vers  mais ne
diverge pas pour
mais ne
diverge pas pour  qui tend vers
qui tend vers  .
.
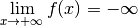
Remarque 3.6.19. Il existe une quantité non négligeable de résultats intéressants portant
sur les limites et les divergences de fonctions pour  qui tend
vers
qui tend
vers  ou vers
ou vers  . Néanmoins, dans ce cours,
nous nous contenterons d’utiliser ces notions comme des outils qui
permettent de décrire le comportement asymptotique d’une fonction.
. Néanmoins, dans ce cours,
nous nous contenterons d’utiliser ces notions comme des outils qui
permettent de décrire le comportement asymptotique d’une fonction.
Passons aux exercices.
Exercice 3.6.20. (Exercice théorique un peu difficile.)
Les définitions 3.6.3 et 3.6.4 sont très similaires. Identifier la seule petite différence et expliquer celle-ci.
Exercice 3.6.21. Tracer le graphe d’une fonction  ayant les propriétés suivantes
:
ayant les propriétés suivantes
:
Solution.
Exercice 3.6.22. Déterminer si les fonctions dont les graphes sont donnés ci-dessous
ont une limite ou divergent pour  qui tend vers
qui tend vers
 ou
ou  .
.








Exercice 3.6.23. Déterminer si les fonctions convergent ou divergent pour  qui
tend vers
qui
tend vers  ou pour
ou pour  qui tend vers
qui tend vers
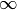 . Si elles convergent, donner la limite. Si elles
divergent, donner le type de divergence (vers
. Si elles convergent, donner la limite. Si elles
divergent, donner le type de divergence (vers  ou vers
ou vers
 ). N’hésitez pas à vous aider d’un graphe.
). N’hésitez pas à vous aider d’un graphe.






Exercice 3.6.24. Un homme souhaite changer la teneur en sel de son aquarium pour y accueillir de nouveaux poissons. Alors que son aquarium contient initialement 3 litres d’eau douce, il commence à remplir l’aquarium avec à la fois de l’eau douce et de l’eau salée (avec deux pompes différentes). La pompe d’eau douce a un débit d’un centilitre par seconde, tandis que la pompe d’eau salée a un débit de deux centilitres par seconde.
Quel est le rapport de la quantité d’eau douce et de la quantité d’eau salée après une minute de remplissage ?
Quel est le rapport de la quantité d’eau douce et de la quantité d’eau salée après
 secondes de remplissage ? (
secondes de remplissage ? (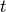 étant un nombre réel strictement positif quelconque.)
étant un nombre réel strictement positif quelconque.)Au fur et à mesure que le temps passe, de quoi se rapproche le rapport de la quantité d’eau douce et de la quantité d’eau salée ?

Exercice 3.6.25. Un avion a une panne de moteur en plein vol à une altitude de
 km et menace de s’écraser. Le pilote va essayer de faire
planer l’avion jusqu’au prochain aréoport, mais il craint que l’avion
perde trop d’altitude en planant.
km et menace de s’écraser. Le pilote va essayer de faire
planer l’avion jusqu’au prochain aréoport, mais il craint que l’avion
perde trop d’altitude en planant.
Il se souvient de ses cours d’aviation que dans ce genre de situation,
l’avion perd d’abord rapidement beaucoup d’altitude mais se stabilise
peu à peu. Il se souvient que dans ce genre de situation, l’altitude
de l’avion après 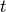 heures est de
heures est de 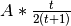 où
où
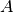 est l’altitude initiale de l’avion.
est l’altitude initiale de l’avion.
De quelle altitude se rapproche de l’avion au fur et à mesure que le temps passe ? Risque-t-il de s’écraser ?

3.7 Asymptotes¶
Exemple 3.7.1. Voici ci-dessous le graphe de la fonction :
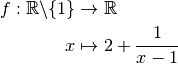
Les limites et les divergences intéressantes pour cette fonction sont :


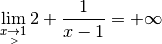
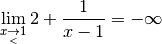
Rappelons-nous ce que signifie en français la première de ces quatre
affirmations : au fur et à mesure que  devient grand, les
nombres
devient grand, les
nombres 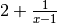 associées se rapprochent uniformément et
définitivement de
associées se rapprochent uniformément et
définitivement de  . Une autre façon d’exprimer cela, plus
géométrique, est de dire que plus on considère des points du graphe de
la fonction
. Une autre façon d’exprimer cela, plus
géométrique, est de dire que plus on considère des points du graphe de
la fonction  dont les abscisses sont grandes, plus le graphe de
dont les abscisses sont grandes, plus le graphe de
 se rapproche uniformément et définitivement de la droite
d’équation
se rapproche uniformément et définitivement de la droite
d’équation 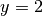 :
:
 . Son sens est exactement celui encodé par la limite
. Son sens est exactement celui encodé par la limite
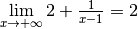 .
.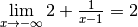 peut également
être interprétée géométriquement avec une asymptote horizontale : plus
on considère des points du graphe de la fonction
peut également
être interprétée géométriquement avec une asymptote horizontale : plus
on considère des points du graphe de la fonction  dont les
abscisses sont petites, plus le graphe de
dont les
abscisses sont petites, plus le graphe de  se rapproche
uniformément et définitivement de la droite d’équation
se rapproche
uniformément et définitivement de la droite d’équation 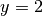 également.
également.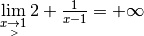 et
et
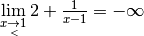 de
façon plus géométrique, il faut recourir à la notion d’asymptote
verticale. Pour cet exemple, on dira que la focntion a une asymptote
verticale d’équation cartésienne
de
façon plus géométrique, il faut recourir à la notion d’asymptote
verticale. Pour cet exemple, on dira que la focntion a une asymptote
verticale d’équation cartésienne 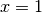 :
:Plus on on considère des points du graphe de  dont les
abscisses sont proches de
dont les
abscisses sont proches de  , plus le graphe de
, plus le graphe de  se
rapproche uniformément et définitivement de cette droite. Le sens de
cette asymptote verticale est exactement celui des deux divergences
se
rapproche uniformément et définitivement de cette droite. Le sens de
cette asymptote verticale est exactement celui des deux divergences
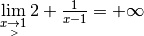 et
et
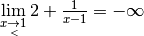 .
.
Les asymptotes horizontales sont donc juste une manière plus géométrique
d’exprimer des limites pour  qui tend vers
qui tend vers  ou
ou
 de fonctions et les asymptotes verticales sont juste une
manière plus géométrique d’exprimer des divergences en un point de
fonctions. Donnons les définitions précises de ces deux nouvelles
notions.
de fonctions et les asymptotes verticales sont juste une
manière plus géométrique d’exprimer des divergences en un point de
fonctions. Donnons les définitions précises de ces deux nouvelles
notions.
Définition 3.7.2. Soit un intervalle  non majoré. Soit
non majoré. Soit  .
.
Si
, on dit que
a une asymptote horizontale (à droite) d’équation cartésienne
et on note :
Définition 3.7.3. Soit un intervalle  non minoré. Soit
non minoré. Soit  .
.
Si
, on dit que
a une asymptote horizontale (à gauche) d’équation cartésienne
et on note :
Définition 3.7.4. Soit un intervalle  éventuellement privé d’un point
éventuellement privé d’un point  . Soit
. Soit  .
.
Si
ou
, on dit que
a une asymptote verticale (à droite) d’équation cartésienne
et on note :
Définition 3.7.5. Soit un intervalle  éventuellement privé d’un point
éventuellement privé d’un point  . Soit
. Soit  .
.
Si
ou
, on dit que
a une asymptote verticale (à gauche) d’équation cartésienne
et on note :
Remarque 3.7.6. Il existe encore au moins un autre type d’asymptote : les asymptotes obliques. Nous n’en parlerons pas dans ce cours.
Puisque les asymptotes ne sont qu’une réinterprétation géométrique de certaines limites, il n’y a pas grand chose d’autre à dire à leur sujet. Passons donc immédiatement aux exercices.
Exercice 3.7.7. Pour les fonctions dont les graphes sont donnés ci-dessous, lister toutes les asymptotes horizontales et verticales et donner leurs équations cartésiennes.




Exercice 3.7.8. Donner le graphe d’une fonction qui possède deux asymptotes horizontales
(différentes), deux asymptotes verticales dont une des deux a pour
équation cartésienne 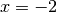 . Donner les équations cartésiennes de
toutes les asympotes horizontales et verticales de la fonction choisie.
. Donner les équations cartésiennes de
toutes les asympotes horizontales et verticales de la fonction choisie.
Solution.
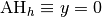


Exercice 3.7.9. Pour les fonctions suivantes, déterminer les équations cartésiennes de toutes les asymptotes horizontales et verticales.






3.8 Propriétés des limites de fonctions¶
Exemple 3.8.1. À ce stade, nous savons déjà que la fonction inverse converge
vers  pour
pour  qui tend vers
qui tend vers  :
:
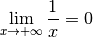
De même, nous savons que la fonction constante de constante  converge vers
converge vers  :
:

Question : à partir de ces deux informations, pouvons-nous affirmer
quelque chose au sujet du comportement asymptotique (pour  qui
tend vers
qui
tend vers  ) de la fonction obtenue en additionnant ces
deux premières fonctions :
) de la fonction obtenue en additionnant ces
deux premières fonctions :

Bien entendu, calculer directement la limite pour  qui tend
vers
qui tend
vers  de cette fonction
de cette fonction  n’est pas difficile :
n’est pas difficile :
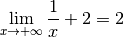
Mais aurions-nous pu trouver ce résultat sans même réfléchir au
comportement asymptotique de la fonction  ? Pour répondre à
cette question, rappelons ce que signifient les deux affirmations :
? Pour répondre à
cette question, rappelons ce que signifient les deux affirmations :
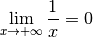

La première signifie que pour des nombres  de plus en plus
grands, les nombres
de plus en plus
grands, les nombres 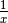 se rapprochent uniformément et
définitivement de
se rapprochent uniformément et
définitivement de  . La deuxième signifie que pour des nombres
. La deuxième signifie que pour des nombres
 de plus en plus grands, les nombres
de plus en plus grands, les nombres  se rapprochent
uniformément et définitivement de
se rapprochent
uniformément et définitivement de  . On déduit directement de
ces deux informations que pour des nombres
. On déduit directement de
ces deux informations que pour des nombres  de plus en plus
grands, les nombres
de plus en plus
grands, les nombres 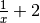 se rapprochent uniformément et
définitivement de
se rapprochent uniformément et
définitivement de 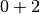 . Autrement dit :
. Autrement dit :
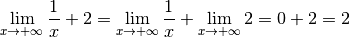
La limite pour  qui tend vers
qui tend vers  de la fonction
de la fonction
 qui est définie comme la somme de la fonction inverse et de la
fonction constante de constante
qui est définie comme la somme de la fonction inverse et de la
fonction constante de constante  est égale à la somme des
limites pour
est égale à la somme des
limites pour  qui tend vers
qui tend vers  de ces deux
fonctions. On a pu décomposer le calcul de la limite pour
de ces deux
fonctions. On a pu décomposer le calcul de la limite pour  qui
tend vers
qui
tend vers  de la fonction
de la fonction  en une somme de
limites plus simples à calculer.
en une somme de
limites plus simples à calculer.
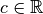 .
.Proposition 3.8.2. Soit  un intervalle éventuellement privé d’un point
un intervalle éventuellement privé d’un point  .
.
Soient
et
telles que
et
. Alors la fonction
a une limite en
et on a :
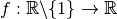 et
et
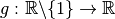 dont les graphes
sont les suivants :
dont les graphes
sont les suivants :Ces deux fonctions ont toutes les deux une limite en  :
:
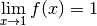
Que se passe-t-il si nous nous créons une nouvelle fonction en
additionnant  et
et  :
:
 .
.
 a également une limite en
a également une limite en  et cette
limite est la somme des limites en
et cette
limite est la somme des limites en  des fonctions
des fonctions  et
et  :
:  .
. se rapproche uniformément et
définitivement de
se rapproche uniformément et
définitivement de  à l’approche de
à l’approche de  et que la
fonction
et que la
fonction  se rapproche uniformément et définitivement de
se rapproche uniformément et définitivement de
 à l’approche de
à l’approche de  , la fonction
, la fonction  qui est la
somme de ces deux fonctions se rapproche uniformément et
définitivement de
qui est la
somme de ces deux fonctions se rapproche uniformément et
définitivement de  à l’approche de
à l’approche de  . Cette
remarque n’est évidemment pas propre à notre exemple : il en aurait
été de même pour d’autres fonctions
. Cette
remarque n’est évidemment pas propre à notre exemple : il en aurait
été de même pour d’autres fonctions  et
et  . C’est ce
qui est exactement exprimé par la proposition
3.8.2.
. C’est ce
qui est exactement exprimé par la proposition
3.8.2.Exemple 3.8.3. Supposons que l’on souhaite déterminer si la fonction suivante possède
une limite en  .
.
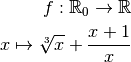
On remarque que la fonction  est la somme des trois fonctions :
est la somme des trois fonctions :
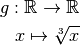
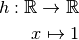
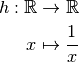
De plus, on sait facilement calculer les limites en  de ces
trois fonctions :
de ces
trois fonctions :
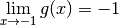
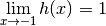

Par la proposition 3.8.2,  a donc
nécessairement une limite en
a donc
nécessairement une limite en  et cette limite est égale à :
et cette limite est égale à :
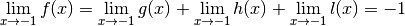
La proposition 3.8.2 décrit ce qu’il se passe lorsqu’on additionne deux fonctions qui possèdent une limite en un point. Il existe bien évidemment d’autres opérations sur les fonctions et d’autres possibilités pour une fonction que d’avoir une limite en un point (elle peut par exemple diverger). Dans les pages suivantes, nous allons donner toutes les variantes possibles de la proposition 3.8.2. Insistons sur un point : n’apprennez pas toutes ces propositions par cœur ! Comprenez-les de sorte que vous puissiez les retrouver par vous-mêmes.
Proposition 3.8.4. Soit  un intervalle éventuellement privé d’un point
un intervalle éventuellement privé d’un point  .
.
Soient
et
telles que
et
. Alors la fonction
a une limite en
et on a :
Proposition 3.8.5. Soit  un intervalle éventuellement privé d’un point
un intervalle éventuellement privé d’un point  .
.
Soient
et
telles que
et
. Alors la fonction
a une limite en
et on a :
- Proposition 3.8.6. Soit
 un intervalle éventuellement privé d’un point
un intervalle éventuellement privé d’un point  .
Soient
.
Soient  et
et  avec
avec  pour tout
pour tout 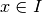 telles que
telles que
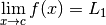 et
et
 avec
avec  .
Alors la fonction
.
Alors la fonction 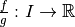 a une limite
en
a une limite
en  et on a :
et on a :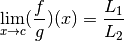
Proposition 3.8.7. Soit  un intervalle éventuellement privé d’un point
un intervalle éventuellement privé d’un point  et soit
et soit 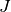 un intervalle éventuellement privé d’un point
un intervalle éventuellement privé d’un point  .
.
Soient
et
telles que
,
et
. Alors la fonction
a une limite en
et on a :
Passons aux cas où la fonction  diverge vers
diverge vers  .
.
Proposition 3.8.8. Soit  un intervalle éventuellement privé d’un point
un intervalle éventuellement privé d’un point  .
.
Soient
et
telles que
et
. Alors la fonction
diverge en
et on a :
Proposition 3.8.9. Soit  un intervalle éventuellement privé d’un point
un intervalle éventuellement privé d’un point  .
.
Soient
et
telles que
et
. Alors la fonction
diverge en
et on a :
Proposition 3.8.10. Soit  un intervalle éventuellement privé d’un point
un intervalle éventuellement privé d’un point  .
.
Soient
et
telles que
avec
et
. Alors la fonction
diverge en
et on a :
Si
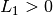 :
: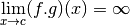
Si
 :
: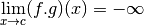
Proposition 3.8.11. Soit  un intervalle éventuellement privé d’un point
un intervalle éventuellement privé d’un point  .
.
Soient
et
avec
pour tout
telles que
et
. Alors la fonction
a une limite en
et on a :
Proposition 3.8.12. Soit  un intervalle non majoré et soit
un intervalle non majoré et soit 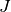 un intervalle éventuellement privé d’un point
un intervalle éventuellement privé d’un point  .
.
Soient
et
telles que
,
et
. Alors la fonction
a une limite en
et on a :
Les cas où la fonction  diverge vers
diverge vers  sont très
similaires aux cinq précédents et nous ne les listerons pas ici. Passons
aux cas où la fonction
sont très
similaires aux cinq précédents et nous ne les listerons pas ici. Passons
aux cas où la fonction  diverge vers
diverge vers  mais où la
fonction
mais où la
fonction  converge.
converge.
Proposition 3.8.13. Soit  un intervalle éventuellement privé d’un point
un intervalle éventuellement privé d’un point  .
.
Soient
et
telles que
et
. Alors la fonction
diverge en
et on a :
Proposition 3.8.14. Soit  un intervalle éventuellement privé d’un point
un intervalle éventuellement privé d’un point  .
.
Soient
et
telles que
et
. Alors la fonction
diverge en
et on a :
Proposition 3.8.15. Soit  un intervalle éventuellement privé d’un point
un intervalle éventuellement privé d’un point  .
.
Soient
et
telles que
avec
et
. Alors la fonction
diverge en
et on a :
Si
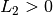 :
: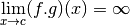
Si
 :
: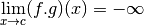
Proposition 3.8.16. Soit  un intervalle éventuellement privé d’un point
un intervalle éventuellement privé d’un point  .
.
Soient
et
avec
pour tout
telles que
et
. Alors la fonction
diverge en
et on a :
Si
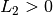 :
: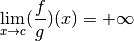
Si
 :
: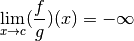
Proposition 3.8.17. Soit  un intervalle éventuellement privé d’un point
un intervalle éventuellement privé d’un point  et soit
et soit 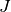 un intervalle éventuellement privé d’un point
un intervalle éventuellement privé d’un point
 .
.
Soient
et
telles que
,
et
. Alors la fonction
diverge en
et on a :
À nouveau, les cas où la fonction  diverge vers
diverge vers  sont très similaires aux cinq précédents et nous ne les listerons pas
ici. Passons aux cas où la fonction
sont très similaires aux cinq précédents et nous ne les listerons pas
ici. Passons aux cas où la fonction  diverge vers
diverge vers
 et où la fonction
et où la fonction  diverge vers
diverge vers
 .
.
Proposition 3.8.18. Soit  un intervalle éventuellement privé d’un point
un intervalle éventuellement privé d’un point
 .
.
Soient
et
telles que
et
. Alors la fonction
diverge en
et on a :
Proposition 3.8.19. Soit  un intervalle éventuellement privé d’un point
un intervalle éventuellement privé d’un point
 .
.
Soient
et
telles que
avec
et
. Alors la fonction
diverge en
et on a :
Proposition 3.8.20. Soit  un intervalle non majoré et soit
un intervalle non majoré et soit 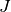 un
intervalle éventuellement privé d’un point
un
intervalle éventuellement privé d’un point  .
.
Soient
et
telles que
,
et
. Alors la fonction
diverge en
et on a :
Les cas où la fonction  ou la fonction
ou la fonction  diverge vers
diverge vers
 plutôt que vers
plutôt que vers  sont très similaires aux
cinq derniers et nous ne les listerons pas ici. Tous les cas où on ne
considère pas une limite ou une divergence en un point mais pour
sont très similaires aux
cinq derniers et nous ne les listerons pas ici. Tous les cas où on ne
considère pas une limite ou une divergence en un point mais pour
 qui tend vers
qui tend vers  ou vers
ou vers  sont
semblables à ceux que nous avons déjà listés, nous ne les listerons donc
pas ici.
sont
semblables à ceux que nous avons déjà listés, nous ne les listerons donc
pas ici.
Remarque 3.8.21. Il peut sembler que certaines propositions sont manquantes. Par
exemples, quid de la différence de deux fonctions qui divergent vers
 en un point
en un point  ?
Une personne peu rigoureuse pourrait écrire que :
?
Une personne peu rigoureuse pourrait écrire que :

Outre le fait que cela n’a aucun sens, cela est absolument faux ! Je vous interdis de noter de telles horreurs dans le cadre de ce cours.
Ce type de situation est appelé par certaines personnes indétermination . Une indétermination est en fait une situation où on ne peut pas simplement appliquer une des propositions listées ci-dessus pour décomposer une limite ou une divergence que l’on cherche à calculer. Il faut dans ces cas-là ruser, simplifier l’expression de la fonction considérée ou même être imaginatif ! Toutes sortes de choses peuvent arriver !
Illustrons cette dernière affirmation. Commençons par donner un
exemple de deux fonctions qui divergent vers  en un
point mais dont la différence ne converge pas vers
en un
point mais dont la différence ne converge pas vers  , elle
diverge vers
, elle
diverge vers  .
.
Considérons les deux fonctions :
On a :
Pour tout
, on a :
La fonction
peut être vue comme le produit des deux fonctions :
On a :
Par la proposition 3.8.10, on en déduit que :
À présent, donnons un exemple de deux fonctions qui divergent vers
en un point mais dont la différence diverge vers
. Considérons les deux fonctions :
On a :
Pour tout
, on a :
La fonction
peut être vue comme le produit des deux fonctions :
On a :
Par la proposition 3.8.10, on en déduit que :
Enfin, la différence de deux fonctions qui divergent vers
en un point peut malgré tout parfois converger (vers
ou un autre nombre). Considérons par exemple les deux fonctions :
On a :
Pour tout
, on a :
On en déduit :
Comme on peut le voir avec ces trois exemples, lorsqu’on est face à une indétermination, il n’y a pas d’autre choix que de se mettre à réfléchir. Il n’y a pas de loi générale.
 qui tend
vers
qui tend
vers  (ou vers
(ou vers  ) dans le cas d’une
fonction rationnelle (quotient de deux polynômes).
) dans le cas d’une
fonction rationnelle (quotient de deux polynômes).Théorème 3.8.22. (Théorème de la règle des plus hautes puissances)
 un intervalle non majoré.
un intervalle non majoré. et
et  avec
avec  pour tout
pour tout 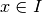 telles que pour
tout
telles que pour
tout 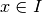 :
:
pour un certain
, un certain
et
avec
et
avec
. Alors :
- Si
,
on a :
- Si
,
on a :
- Si
pour un certain
, on a :
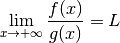
Démonstration Pour tout  avec
avec  , on a :
, on a :

Par les propriétés des limites, on a :


De même :
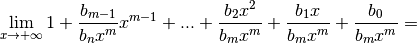
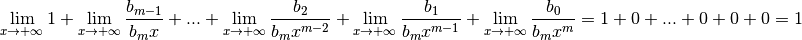
Par les propriétés des limites, on a donc :
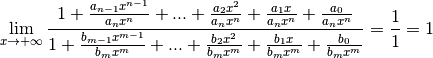
Dès lors :
Si
 ,
par les propriétés des limites et des divergences, on a :
,
par les propriétés des limites et des divergences, on a :
Si
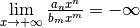 ,
par les propriétés des limites et des divergences, on a :
,
par les propriétés des limites et des divergences, on a :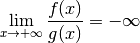
Si
 pour un certain
pour un certain  , par les propriétés des
limites, on a :
, par les propriétés des
limites, on a :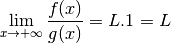
Remarque 3.8.23. Le théorème est également valable lorsqu’on considère une limite pour
 qui tend vers
qui tend vers  .
.
Exemple 3.8.24. On souhaite déterminer la limite suivante :

Le théorème de la règle des plus hautes puissances nous dit que si la limite ci-dessous existe, alors la limite que nous recherchons existe aussi et est égale à celle-ci :
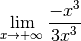
Or :
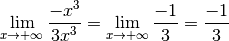
Conclusion, par le théorème de la règle des plus hautes puissances, on déduit que :

Exercice 3.8.25. Soit  un intervalle éventuellement privé d’un point
un intervalle éventuellement privé d’un point
 . Soient
. Soient  et
et
 telles que
telles que
 et
et
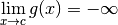 .
.
Que peut-on dire au sujet du comportement de la fonction
 au voisinage de
au voisinage de  ?
Converge-t-elle ? Diverge-t-elle ? Expliquer.
?
Converge-t-elle ? Diverge-t-elle ? Expliquer.
Solution. Puisque  , pour des nombres
, pour des nombres
 de plus en plus proches de
de plus en plus proches de  , les nombres
, les nombres  deviennent uniformément et définitivement arbitrairement grands. Puisque
deviennent uniformément et définitivement arbitrairement grands. Puisque
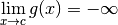 , pour des nombres
, pour des nombres  de plus en plus proches de
de plus en plus proches de  , les nombres
, les nombres 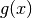 deviennent uniformément et définitivement arbitrairement petits. Dès
lors, pour des nombres
deviennent uniformément et définitivement arbitrairement petits. Dès
lors, pour des nombres  de plus en plus proches de
de plus en plus proches de  ,
les nombres
,
les nombres  deviennent uniformément et définitivement
arbitrairement petits (le produit de nombres de plus en plus grands par
des nombres petits est de plus en plus petit).
deviennent uniformément et définitivement
arbitrairement petits (le produit de nombres de plus en plus grands par
des nombres petits est de plus en plus petit).
Exercice 3.8.26. Soit  un intervalle non minoré. Soient
un intervalle non minoré. Soient
 et
et  avec
avec
 pour tout
pour tout 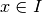 telles que
telles que
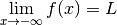 pour un certain
pour un certain
 et
et
 .
.
Que peut-on dire au sujet du comportement de la fonction
 pour
pour  qui tend vers
qui tend vers
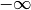 ? Converge-t-elle ? Diverge-t-elle ? Expliquer.
? Converge-t-elle ? Diverge-t-elle ? Expliquer.
Solution. Puisque 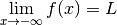 , pour des nombres
, pour des nombres
 de plus en plus petits, les nombres
de plus en plus petits, les nombres  se
rapprochent uniformément et définitivement de
se
rapprochent uniformément et définitivement de 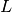 . Puisque
. Puisque
 , pour des nombres
, pour des nombres
 de plus en plus petits, les nombres
de plus en plus petits, les nombres  deviennent
uniformément et définitivement arbitrairement petits. Dès lors, pour des
nombres
deviennent
uniformément et définitivement arbitrairement petits. Dès lors, pour des
nombres  de plus en plus petits, les nombres
de plus en plus petits, les nombres
 se rapprochent uniformément et définitivement
de
se rapprochent uniformément et définitivement
de  (le quotient de nombres de plus en plus proche d’un nombre
(le quotient de nombres de plus en plus proche d’un nombre
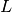 divisés par des nombres de plus en plus petits est de plus en
plus proche de
divisés par des nombres de plus en plus petits est de plus en
plus proche de  ).
).
Exercice 3.8.27. Soit  un intervalle non majoré. Soient
un intervalle non majoré. Soient
 et
et  avec
avec
 pour tout
pour tout 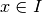 telles que
telles que
 et
et
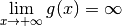 .
.
Que peut-on dire au sujet du comportement de la fonction
 pour
pour  qui tend vers
qui tend vers
 ? Converge-t-elle ? Diverge-t-elle ? Expliquer.
? Converge-t-elle ? Diverge-t-elle ? Expliquer.
Solution. Puisque  , pour des
nombres
, pour des
nombres  de plus en plus grands, les nombres
de plus en plus grands, les nombres  deviennent uniformément et définitivement arbitrairement petits. Puisque
deviennent uniformément et définitivement arbitrairement petits. Puisque
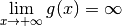 , pour des nombres
, pour des nombres
 de plus en plus grands, les nombres
de plus en plus grands, les nombres 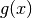 deviennent
uniformément et définitivement arbitrairement grands. Dès lors, pour des
nombres
deviennent
uniformément et définitivement arbitrairement grands. Dès lors, pour des
nombres  de plus en plus petits, les nombres
de plus en plus petits, les nombres  deviennent uniformément et définitivement arbitrairement petits (des
nombres de plus en plus petits auquels on enlève des nombres de plus en
plus grands donnent de plus en plus petits).
deviennent uniformément et définitivement arbitrairement petits (des
nombres de plus en plus petits auquels on enlève des nombres de plus en
plus grands donnent de plus en plus petits).
Exercice 3.8.28. En utilisant les propriétés des limites et des divergences, déterminer les limites ou les divergences suivantes.










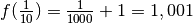
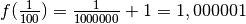


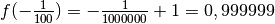
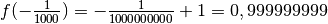
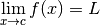
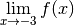
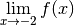
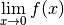


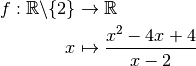
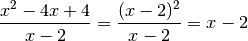
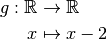



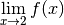

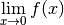
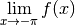


 .
.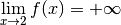 .
.