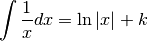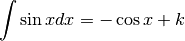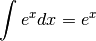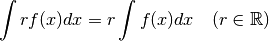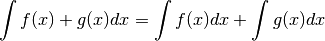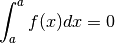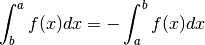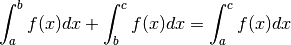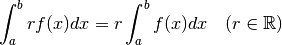Théorie¶
1. Primitive¶
Définition¶
Soit  une fonction réelle définie sur un intervalle réel
une fonction réelle définie sur un intervalle réel
 .
.  est primitivable sur
est primitivable sur  s’il existe une
fonction
s’il existe une
fonction 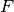 de
de 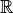 dans
dans 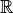 ,
dérivable sur
,
dérivable sur  et telle que
et telle que

Une telle fonction s’appelle une primitive de  sur
sur  .
.
Proposition¶
Soit  de
de 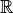 dans
dans 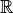 primitivable sur l’intervalle réel
primitivable sur l’intervalle réel  . Si
. Si 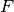 est une
primitive de
est une
primitive de  sur
sur  ,
,
alors 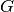 de
de  dans
dans  est une
primitive de
est une
primitive de  sur
sur  si et seulement si F-G est
constante sur I.
si et seulement si F-G est
constante sur I.
À la figure 1, on a représenté une fonction. A la figure 2, on peut voir quelques primitives de cette fonction sur l’intervalle [-3,3].
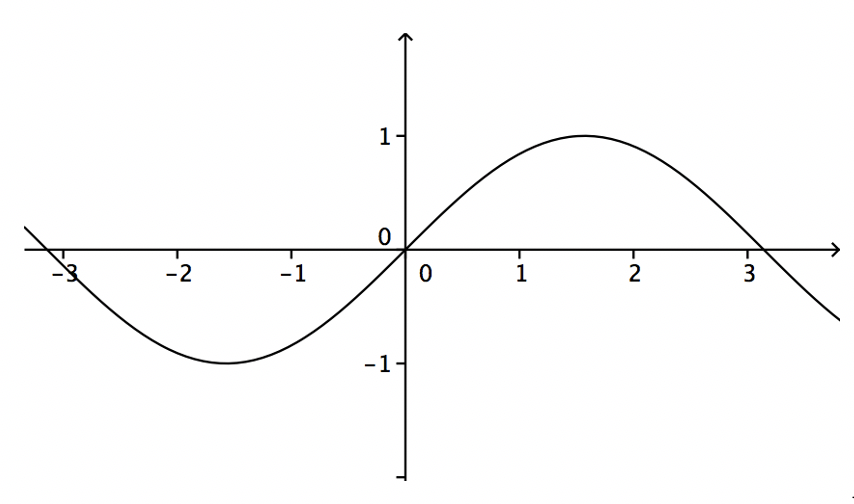
Figure 1¶

Figure 2¶
On note
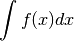
l’ensemble des primitives de la fonction  sur un intervalle
donné.
sur un intervalle
donné.
Primitivation par parties¶
Soient  et
et 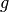 deux fonctions à valeurs dans
deux fonctions à valeurs dans
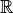 , dérivables sur un intervalle
, dérivables sur un intervalle  réel. Alors
réel. Alors
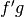 est primitivable sur
est primitivable sur  si et seulement si
si et seulement si
 l’est, auquel cas
l’est, auquel cas
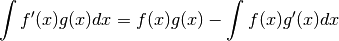
La démonstration se déduit de la formule de dérivation de 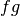 .
Comme
.
Comme
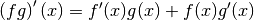
On peut en déduire, en utilisant la propriété (2) du paragraphe 1.5, que
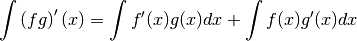
Ce qui nous conduit aisément à l’égalité à démontrer.
Illustrons cette méthode de primitivation par un exemple. Soit à calculer
Si on pose 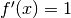 ,
, 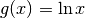 , il en résulte que
, il en résulte que
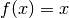 ,
, 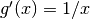 et grâce au théorème de primitivation
par partie, on a :
et grâce au théorème de primitivation
par partie, on a :

Primitivation par substitution¶
La dérivée de la composée de deux fonctions est un produit. Si la
fonction  est dérivable en une valeur
est dérivable en une valeur 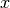 de son domaine,
si la fonction
de son domaine,
si la fonction 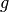 est définie et dérivable en f(x),
est définie et dérivable en f(x),
alors 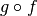 est dérivable en
est dérivable en 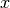 et
et
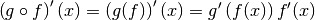
Si on primitive les deux membres de l’égalité, sachant qu’une primitive de la dérivée d’une fonction est la fonction elle même, on a
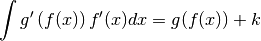
Pourquoi parle-t-on de substitution? Parce qu’une façon de faire
consiste à substituer une variable 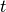 à la variable
à la variable 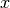 .
Pratiquement, on pose
.
Pratiquement, on pose  . Comme
. Comme  exprime la
variation de
exprime la
variation de 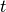 par rapport à
par rapport à 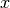 , on écrit encore que
, on écrit encore que
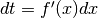 , que l’on nomme différentielle.
, que l’on nomme différentielle.
Ce qui nous conduit à une reformulation de l’égalité (4):
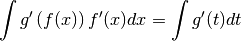
Une fois la primitivation en 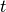 effectuée, on remplace
effectuée, on remplace 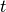 par sa valeur en fonction de
par sa valeur en fonction de 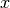 .
.
Deux primitivations particulières s’avèrent presque immédiates à la suite du résultat (4):
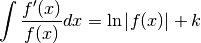
Dans ce cas 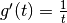 .
.
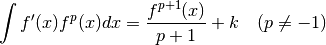
Dans ce cas 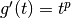 .
.
Illustrons le première. Soit à calculer

En écrivant la tangente comme quotient du sinus et du cosinus, l’opposé du sinus étant la dérivée du cosinus, on a :
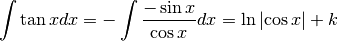
Prenons un autre exemple de substitution qui ne relève pas de ces deux cas particuliers (6) et (7). Soit à calculer
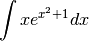
On pose  ,
, 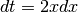 et
et 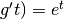 . Dés lors
. Dés lors
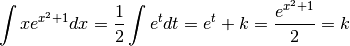
2. Intégrale¶
Pour calculer l’aire sous une courbe, une méthode consiste à approcher cette aire par une somme d’aires de rectangles. Si la fonction est positive et croissante, on peut considérer une fonction en escalier qui minore la fonction (figure 3) et une autre qui la majore (figure 4). En prenant de plus en plus de rectangles ayant des bases d’autant plus petites, on approche d’autant mieux l’aire cherchée.

Figure 3¶
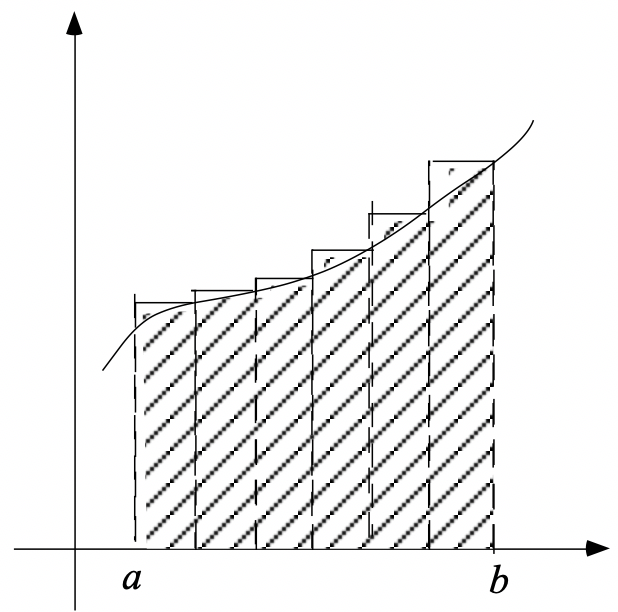
Figure 4¶
Définition¶
Soit  est une fonction définie sur un intervalle réel
est une fonction définie sur un intervalle réel
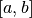 , on divise cet intervalle en
, on divise cet intervalle en  sous-intervalles de
largeur égale 1. Les bornes de ces intervalles sont
sous-intervalles de
largeur égale 1. Les bornes de ces intervalles sont
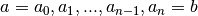
On choisit un valeur à l’intérieur de chaque sous-intervalle

Si  est continue sur
est continue sur 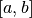 , alors
, alors  est
intégrable sur
est
intégrable sur 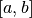 et l’intégrale définie de
et l’intégrale définie de  depuis
depuis
 jusque
jusque  vaut
vaut
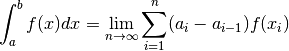
la limite étant indépendante du choix des 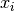 . Dans
l’hypothèse de largeur constante des intervalles, cela devient
. Dans
l’hypothèse de largeur constante des intervalles, cela devient
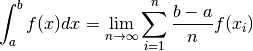
Aire et intégrale¶
Géométriquement, l’intégrale définie 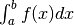 correspond à l’aire comprise entre le graphique de la fonction
correspond à l’aire comprise entre le graphique de la fonction
 , l’axe des abscisses et les droites d’équations
, l’axe des abscisses et les droites d’équations  et
et 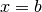 (figure 5) lorsque la fonction est positive.
(figure 5) lorsque la fonction est positive.

Figure 5¶
Par contre, lorsque la fonction est négative (figure 6), l’intégrale est négative. Pour trouver l’aire comprise entre le graphique et l’axe des abscisses, il faut prendre l’opposée de l’intégrale.
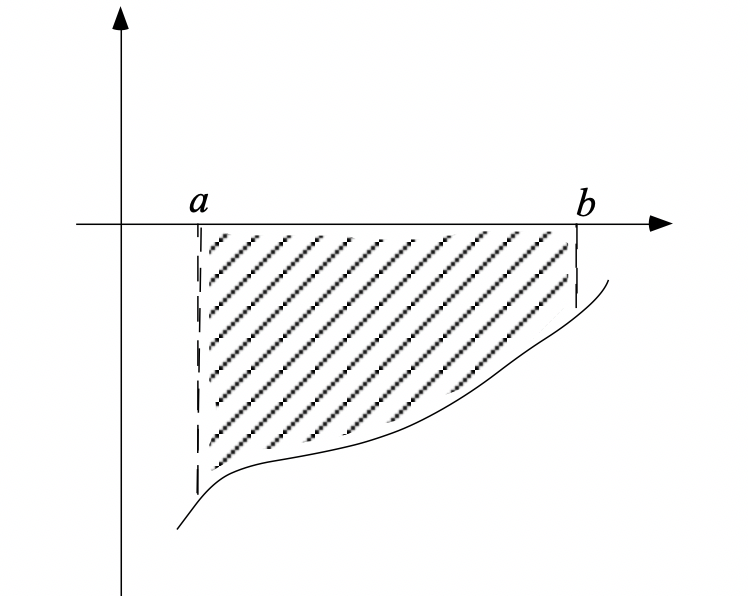
Figure 6¶
Théorème fondamental¶
Si  est une fonction de
est une fonction de 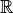 dans
dans
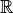 continue et primitivable sur un intervalle
continue et primitivable sur un intervalle
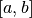 , si
, si 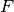 est une primitive de
est une primitive de  sur cet
intervalle, considérons la fonction
sur cet
intervalle, considérons la fonction 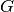 appelée intégrale
généralisée et définie comme suit
appelée intégrale
généralisée et définie comme suit
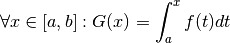
Si  est positive 2,
est positive 2,  est assimilable à l’aire
hachurée de la figure 7. Calculons la dérivée de G, on a
est assimilable à l’aire
hachurée de la figure 7. Calculons la dérivée de G, on a
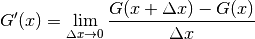

Figure 7¶
Comme toute dérivée, il s’agit de la limite d’un taux d’accroissement.
La différence, au numérateur de ce taux, correspond à l’aire hachurée de
la figure 8, c’est-à-dire l’aire d’un rectangle infinitésimal. Si on
divise cette différence par la largeur  de ce rectangle,
on obtient la hauteur du rectangle, à savoir
de ce rectangle,
on obtient la hauteur du rectangle, à savoir 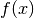 (quand
(quand
 devient très petit). En résumé,
devient très petit). En résumé,
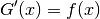

Figure 8¶
Comme  est primitivable,
est primitivable, 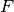 étant une primitive de
étant une primitive de
 , on peut écrire, à partir des propriétés des primitives, que
(
, on peut écrire, à partir des propriétés des primitives, que
( étant un réel)
étant un réel)

ou encore
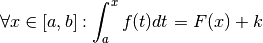
Quand  , on a
, on a

Comme le premier membre de l’égalité est nul, on peut en déduire que
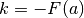
Quand 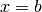 , on a
, on a
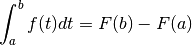
Cela nous donne le moyen de calculer une intégrale définie: pour ce
faire, il faut chercher une primitive de la fonction et la calculer aux
bornes de l’intervalle d’intégration. Prenons un exemple. Soit à
calculer l’aire déterminée par l’axe des abscisses et le graphique de la
fonction sinus entre 0 et 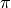 (figure 1). Cette aire est égale à
(figure 1). Cette aire est égale à
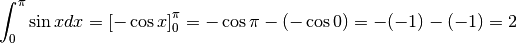
3. Volume¶
Considérons une fonction continue sur un intervalle 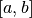 réel.
Considérons également le solide de révolution engendré par la rotation
autour de l’axe
réel.
Considérons également le solide de révolution engendré par la rotation
autour de l’axe 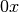 , de la surface plane délimitée par le
graphique de
, de la surface plane délimitée par le
graphique de  et l’axe
et l’axe 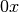 . On veut calculer le volume
de ce solide de révolution. Pour déterminer l’aire sous le graphique, on
a considéré une subdivision de l’intervalle
. On veut calculer le volume
de ce solide de révolution. Pour déterminer l’aire sous le graphique, on
a considéré une subdivision de l’intervalle 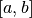 en
en  sous-intervalles et une fonction en escalier (constante sur chaque
sous-intervalle) qui approche la fonction considérée. Si on fait encore
de même, chaque palier de la fonction en escalier va engendrer en
tournant autour de l’axe
sous-intervalles et une fonction en escalier (constante sur chaque
sous-intervalle) qui approche la fonction considérée. Si on fait encore
de même, chaque palier de la fonction en escalier va engendrer en
tournant autour de l’axe 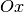 , un cylindre (figure 9) et la
fonction en escalier dans son entièreté engendrera un empilement de
cylindres. Chaque cylindre dont la base est située à l’abscisse x a pour
volume
, un cylindre (figure 9) et la
fonction en escalier dans son entièreté engendrera un empilement de
cylindres. Chaque cylindre dont la base est située à l’abscisse x a pour
volume
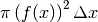
En passant à la limite sur  , on obtiendra le volume du solide
de révolution qui vaut donc
, on obtiendra le volume du solide
de révolution qui vaut donc
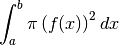
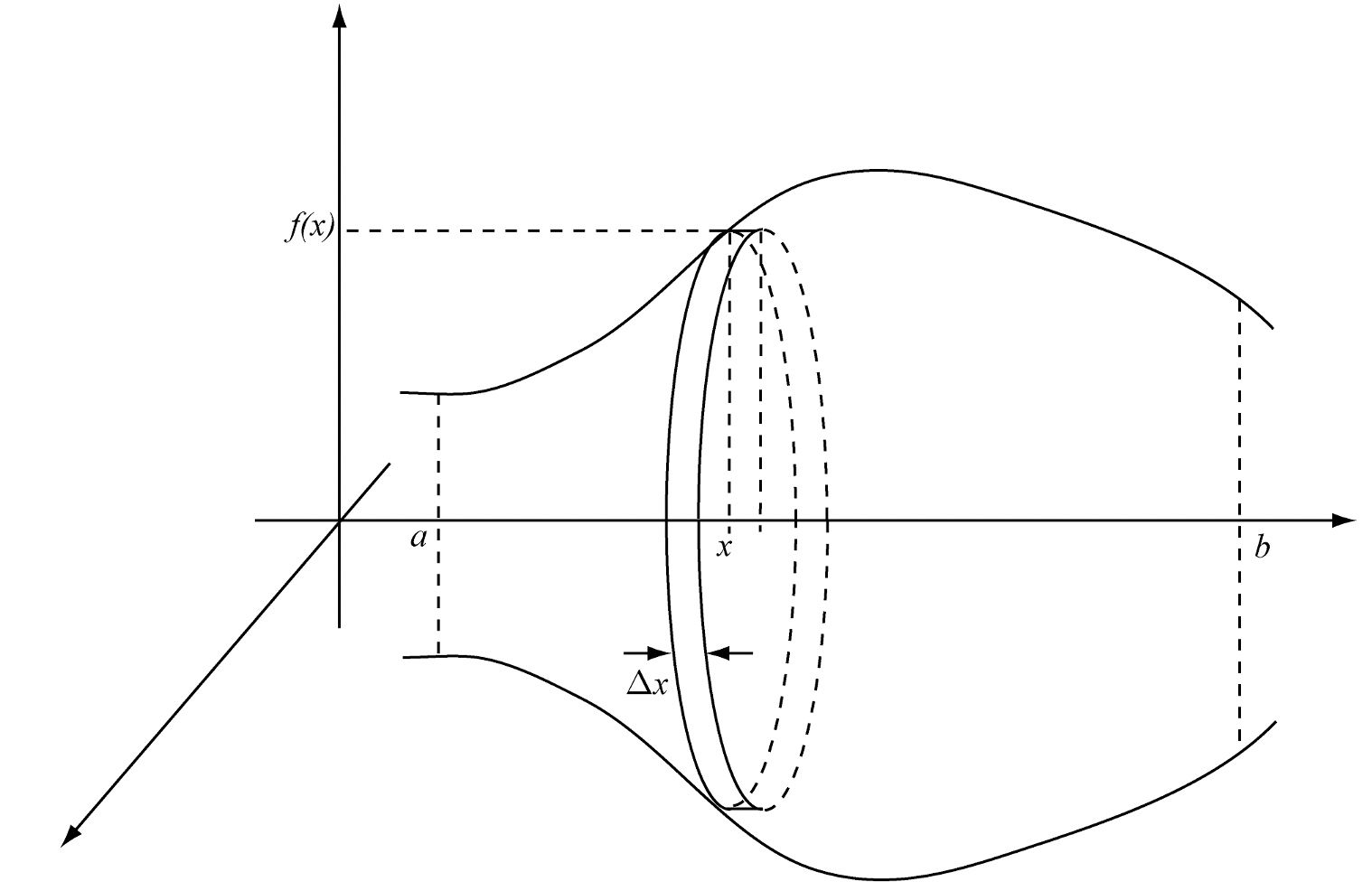
Figure 9¶
4. Mouvements¶
Il a été vu précédemment que, dans un mouvement rectiligne, la vitesse
est obtenue comme dérivée de la position en fonction du temps.
L’accélération est, quant à elle, la dérivée de la vitesse. Dès lors,
pour déterminer la fonction position à partir de la fonction vitesse, il
faut chercher les primitives de la vitesse. Pour déterminer la fonction
vitesse à partir de la fonction accélération, il faut chercher les
primitives de l’accélération. Pour déterminer les constantes  adéquates, on se réfère aux conditions initiales. Considérons, par
exemple, un corps de 10 kg en chute libre, après avoir été lancé avec
une vitesse initiale de 5 m /sec vers le haut et d’une hauteur de 13 m.
Son accélération est celle de la pesanteur, à savoir
adéquates, on se réfère aux conditions initiales. Considérons, par
exemple, un corps de 10 kg en chute libre, après avoir été lancé avec
une vitesse initiale de 5 m /sec vers le haut et d’une hauteur de 13 m.
Son accélération est celle de la pesanteur, à savoir 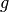 ou -9,81
m/sec. On a donc
ou -9,81
m/sec. On a donc
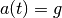
On peut en déduire que
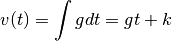
Pour déterminer  , on s’intéresse au temps
, on s’intéresse au temps  . On
sait que la vitesse initiale est de 5 m/sec. D’où
. On
sait que la vitesse initiale est de 5 m/sec. D’où
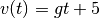
Pour la position, on a
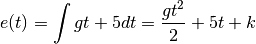
Quand t = 0,
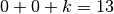
Finalement

- 1
Ce n’est pas obligatoire de prendre une largeur d’intervalle constante sachant que de toutes façons, on fait tendre le nombre d’intervalles vers l’infini et que la largeur de tous les intervalles va tendre vers 0.
- 2
Nous choisissons
 positive pour la facilité du raisonnement
mais le résultat reste le même quel que soit le signe de la fonction.
positive pour la facilité du raisonnement
mais le résultat reste le même quel que soit le signe de la fonction.