3 Fonctions réciproques

Dans cette section, nous allons découvrir les notions et les résultats qui nous permettront de définir les fonctions logarithmes.

3.1 Bijections

Dans un premier temps, intéressons-nous aux fonctions injectives. Grossièrement, les fonctions injectives sont les fonctions qui ne donnent jamais deux fois le même résulat .

Définition 3.1.1. Soit 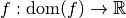une fonction réelle. On dit que est injective si pour tout , si 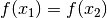, alors .

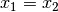Remarque 3.1.2. Géométriquement, dire qu’une fonction réelle 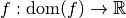est injective revient à dire que son graphe a toujours au plus une intersection avec n’importe quelle droite horizontale.

Exemple 3.1.3. La fonction cubique est injective. En effet, si on a deux nombres 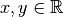tels que 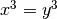, cela implique que 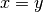. Ils n’existent pas deux nombres différents qui ont le même cube.

Contre-exemple 3.1.4. La fonction carrée n’est pas injective. En effet, si on a deux nombres 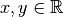tels que 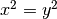, cela n’implique pas nécessairement que 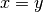. Par exemple, si 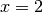et 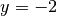, on a 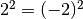sans avoir .

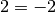Donnons à présent la définition de fonction surjective (sur un ensemble). Intuitivement, dire qu’une fonction est surjective sur un ensemble revient à dire que cette fonction parvient à atteindre tous les éléments de cet ensemble.

Définition 3.1.5. Soit 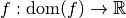une fonction réelle. Soit . On dit que est surjective (sur 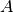) si pour tout 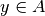, il existe au moins un 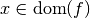tel que .

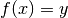Remarque 3.1.6. Par définition de l’image d’une fonction, toute fonction est surjective sur son image.

Exemple 3.1.7. La fonction cubique est surjective sur 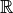. En effet, si on prend 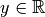, on peut trouver un dans le domaine de la fonction cubique (c’est-à-dire 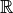) tel que 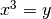: il suffit de prendre .

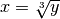Contre-exemple 3.1.8. La fonction carrée n’est pas surjective sur 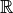. En effet, si on prend 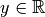, on ne peut pas nécessairement trouver un dans le domaine de la fonction cubique (c’est-à-dire 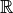) tel que 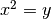: si par exemple 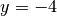, il est impossible de trouver un nombre réel dont le carré vaut 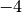. Par contre, la fonction carrée est bien surjective sur son image, c’est-à-dire .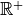

En combiant les notions de fonctions injectives et bijectives, on obtient la notion de bijection.

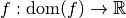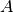Définition 3.1.9. Soit une fonction réelle. Soit . On dit que est une bijective (sur ) si elle est injective et qu’elle est surjective (sur 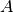). On dit alors que est une bijection (sur ).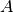

Remarque 3.1.10. Une bijection est une fonction qui associe à tout élément de l’ensemble de départ un unique élément de l’ensemble d’arrivée (comme toute fonction) mais qui réalise également l’inverse : à tout élément de l’ensemble d’arrivée correspond un unique élément de l’ensemble de départ. Une bijection correspond intuitivement à relier chaque élément d’un ensemble avec un élément d’un autre ensemble de sorte que tout élément d’un des deux ensembles ait un unique compagnon dans l’autre ensemble.

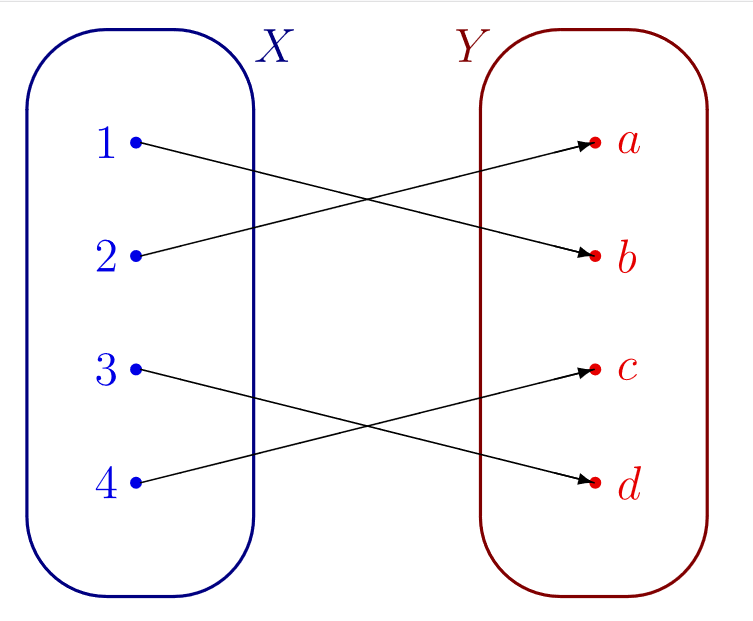
Un exemple graphique de bijection.

Exemple 3.1.11. La fonction cubique est une bijection sur .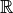

Contre-exemple 3.1.12. La fonction carrée n’est pas une bijection sur 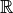car elle n’est pas surjective sur 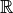, mais elle n’est même pas une bijection sur son image, c’est-à-dire 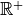, car elle n’est pas injective.

3.2 Fonctions réciproques

Nous pouvons à présent donner la notion qui nous permettra de définir les fonctions logarithmes : celle de fonction réciproque.

Définition 3.2.1. Soit 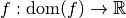une fonction réelle. Une (fonction) réciproque de la fonction est une fonction 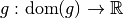telle que 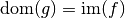et telle que :

1. Pour tout :

   

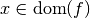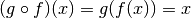
2. Pour tout :

   

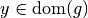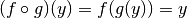
Exemple 3.2.2. La fonction cubique possède une fonction réciproque : la fonction racine cubique. En effet, les domaines de définition et les images de ces deux fonctions sont tous égaux à 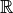et on a :

Pour tout :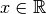

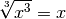
Pour tout :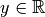

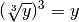
Remarque 3.2.3. D’un point de vue géométrique, trouver une réciproque d’une fonction réelle (qui en possède une) revient à échanger les rôles des abscisses et des ordonnées dans le graphe de la fonction. Autrement dit, le graphe d’une fonction réciproque est toujours le symétrique du graphe de la fonction réelle initiale par la droite d’équation cartésienne (symétrie orthogonale).

Viennent à présent deux résultats que nous ne pourrons tristement pas démontrer dans ce cours (même si leurs démonstrations ne sont pas difficiles) qui permettent de garantir l’existence d’une réciproque d’une fonction donnée à condition que celle-ci soit une bijection, ainsi que son unicité.

Proposition 3.2.4. Soit 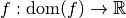une fonction réelle. Alors il existe une réciproque à si et seulement si est une bijection sur son image.

Proposition 3.2.5. Soit 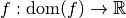une fonction réelle. Si a une réciproque, alors cette réciproque est unique.

Remarque 3.2.6. Étant donné la dernière proposition, on peut parler de LA réciproque d’une fonction réelle 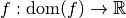sans équivoque. En général, on note cette fonction réciproque 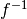, mais nous éviterons d’utiliser cette notation dans ce cours afin d’éviter la confusion avec la notation des exposants.

Il suffit donc qu’une fonction soit une bijection pour qu’elle possède une réciproque. On peut se demander si cette réciproque hérite alors de certaines des propriétés de la fonction de départ. La réponse est donnée par le théorème suivant, que nous ne pourrons pas démontrer dans ce cours.

Définition 3.2.7. (Théorème de la bijection)

Soit un intervalle et soit une fonction réelle.

Si est strictement monotone (c’est-à-dire strictement croissante ou strictement décroissante) et continue, alors est une bijection sur son image et sa fonction réciproque est nécessairement continue. De plus, si est dérivable et que sa dérivée ne s’annule jamais, alors sa fonction réciproque est aussi dérivable.

Ce théorème est la clé qui va nous permettre de définir les fonctions logarithmes. En effet, comme pour tout 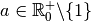, la fonction 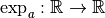est une fonction strictement monotone et continue de 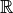dans 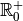, le théorème de la bijection et les propositions 3.2.4 et 3.2.5 nous assurent qu’il existe une unique fonction réciproque à la fonction 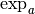. Cette réciproque porte un nom : le logarithme en base .

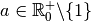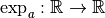Exercice 3.2.8. Le fait que pour , la fonction soit une bijection et donc est injective est très utile pour résoudre des équations qui font intervenir des fonctions exponentielles. En effet, de manière générale, si on a une équation de la forme suivante.

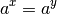
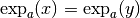
Par injectivité, il suffit alors de résoudre l’équation :

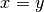
Avant de définir les fonctions logarithmes, familiarisons-nous un peu avec les nouvelles notions de cette section et entraînons-nous à résoudre des équations qui font intervenir des fonctions exponentielles en utilisant l’injectivité de ces fonctions.

3.3 Exercices

Exercice 3.3.1. La fonction inverse est-elle injective ? Si oui, sur quel ensemble est-elle surjective ? Si elle en possède une, quelle est sa fonction réciproque ?

Solution. Oui, elle est injective. Elle est surjective sur 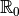. Sa fonction réciproque est elle-même.

Exercice 3.3.2. Démontrer que la composée de deux fonctions injectives définies sur 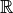est aussi une fonction injective.

Solution. Soien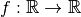t et 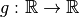deux fonctions injectives. Montrons que la fonction 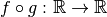est aussi injective. Soient 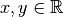. Supposons que . Comme est injective, cela implique que 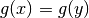. Comm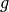e est injective, cela implique que 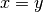. Donc la fonction est injective.

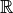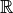Exercice 3.3.3. Les fonctions suivantes sont des bijections de dans . Pour chacune d’entre elles, trouver la fonction réciproque.

Exercice 3.3.4. En utilisant l’injectivité des fonctions exponentielles, résoudre les équations suivantes dans .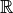

Remarque 3.3.5. Il n’y a pas d’inéquation avec des fonctions exponentielles au programme du cours de mathématiques de 4 heures par semaine. Néanmoins, il est possible que vous ayez à résoudre une telle inéquation ultérieurement, par exemple dans un cours de physique. Si vous souhaitez vous entraîner, prenez les équations de l’exercice 3.3.4 et remplacez les égalités par des inégalités.