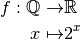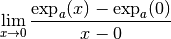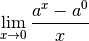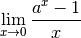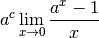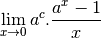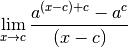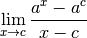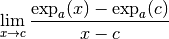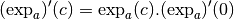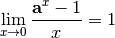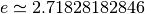2 Fonctions exponentielles¶
2.1 Définition¶
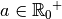 , les exposants naturels, entiers
et rationnels sont déjà définis. On peut donc déjà construire des
fonctions exponentielles sur
, les exposants naturels, entiers
et rationnels sont déjà définis. On peut donc déjà construire des
fonctions exponentielles sur  . Par exemple, si
. Par exemple, si
 , on peut considérer la fonction :
, on peut considérer la fonction :
Dont le graphe est une succession de points non continue :
Nous aimerions étendre cette fonction sur  . Mais pas
de n’importe quelle manière. Un prolongement tel que la fonction :
. Mais pas
de n’importe quelle manière. Un prolongement tel que la fonction :
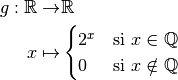
dont le graphe ressemble à :
 qui suit le tracé formé par les points déjà définis . Plus
rigoureusement, nous aimerions que le résultat soit continu, nous
aimerions donc prolonger
qui suit le tracé formé par les points déjà définis . Plus
rigoureusement, nous aimerions que le résultat soit continu, nous
aimerions donc prolonger  de façon continue.
de façon continue.Théorème 2.1.1 (Théorème de prologement par densité).
Soit
une fonction qui est Cauchy-continue.
Alors il existe une unique fonction
qui est un prolongement continu de
sur
.
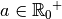 , la fonction :
, la fonction :
est Cauchy-continue, ce qui implique que le théorème de prolongement par densité garantit l’existence d’un unique prolongement continu
de
sur
.
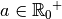 sur
sur
 :
:Définition 2.1.2. Soit 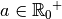 .
.
La fonction exponentielle de base
, notée
, est l’unique prolongement continu sur
de la fonction :
Remarque 2.1.3. Par continuité, le graphe de la fonction
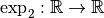 ressemble par exemple à :
ressemble par exemple à :
Cette fois-ci, comme la fonction
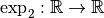 est bien définie sur tout
est bien définie sur tout
 et pas seulement sur
et pas seulement sur  , le graphe de
la fonction est bien un tracé continu.
, le graphe de
la fonction est bien un tracé continu.
Remarque 2.1.4. Pour tout 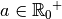 , nous sommes déjà
capables d’évaluer les fonctions
, nous sommes déjà
capables d’évaluer les fonctions  en tout nombre
rationnel. En effet, puisque les fonctions
en tout nombre
rationnel. En effet, puisque les fonctions  sont les
prolongements continus des fonctions exponentielles sur
sont les
prolongements continus des fonctions exponentielles sur
 , si
, si 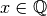 , le nombre
, le nombre
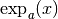 est tout simplement
est tout simplement 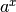 au sens des
exposants rationnels. En particulier, pour tout
au sens des
exposants rationnels. En particulier, pour tout
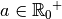 , le nombre
, le nombre 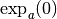 est
est
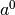 c’est-à-dire
c’est-à-dire  et le nombre
et le nombre 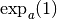 est
est
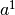 c’est-à-dire
c’est-à-dire  . Géométriquement, cela correspond au
fait que le graphe de toute fonction exponentielle
. Géométriquement, cela correspond au
fait que le graphe de toute fonction exponentielle  passe par les point
passe par les point 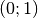 et
et 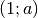 .
.
Notation. Même si elle est au moins dans un premier temps un peu abusive, la
notation suivante est utilisée pour désigner les images des fonctions
 pour
pour 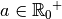 :
:
Pour tout 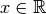 (même quand
(même quand  n’est pas un
nombre rationnel), on note :
n’est pas un
nombre rationnel), on note :
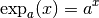
Comme les fonctions exponentielles  sont les
prolongements continus des fonctions exponentielles sur
sont les
prolongements continus des fonctions exponentielles sur
 , il n’est pas étonnant que l’on reprend la notation
des expressions formelles de ces fonctions. Nous verrons que cet abus de
notation prend tout son sens en étudiant les propriétés des fonctions
exponentielles
, il n’est pas étonnant que l’on reprend la notation
des expressions formelles de ces fonctions. Nous verrons que cet abus de
notation prend tout son sens en étudiant les propriétés des fonctions
exponentielles  dans la prochaine section.
dans la prochaine section.
Remarque 2.1.4. Le sens d’une notation telle que 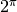 ne vous est donc plus
inconnu. Il s’agit tout simplement de
ne vous est donc plus
inconnu. Il s’agit tout simplement de 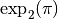 .
Malheureusement, le théorème de prolongement par densité ne nous dit
absolument pas comment calculer cette quantité. Sans la démonstration de
ce théorème, nous ne pouvons même pas estimer ce nombre et cette
nouvelle connaissance du sens de la notation
.
Malheureusement, le théorème de prolongement par densité ne nous dit
absolument pas comment calculer cette quantité. Sans la démonstration de
ce théorème, nous ne pouvons même pas estimer ce nombre et cette
nouvelle connaissance du sens de la notation 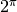 est
honnêtement assez insatisfaisante. Malheureusement, nous ne pourrons pas
remédier à cela dans ce cours.
est
honnêtement assez insatisfaisante. Malheureusement, nous ne pourrons pas
remédier à cela dans ce cours.
2.2 Propriétés élémentaires¶
Listons à présent les propriétés élémentaires de nos nouvelles fonctions
de référence : les fonctions exponentielles. Toutes ces propriétés
découlent directement du fait que les fonctions exponentielles sont
définis comme prolongements continus des fonctions exponentielles sur
 . Malheureusement, nous n’en démontrerons aucune dans
le cadre de ce cours.
. Malheureusement, nous n’en démontrerons aucune dans
le cadre de ce cours.
Proposition 2.2.1. Soit 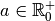 .
Le domaine de définition de la fonction
.
Le domaine de définition de la fonction  est
est  .
.
Proposition 2.2.2. Soit 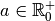 .
.
Si  , l’image de la fonction
, l’image de la fonction  est
est
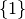 .
.
Si  , l’image de la fonction
, l’image de la fonction  est
est
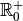 .
.
Proposition 2.2.3. Soit 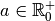 .
.
Si 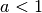 , la fonction
, la fonction  est strictement
décroissante.
est strictement
décroissante.
Si 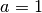 , la fonction
, la fonction  est constante.
est constante.
Si 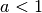 , la fonction
, la fonction  est strictement
croissante.
est strictement
croissante.
Exemple 2.2.4. Par exemple, si 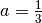 , la fonction
, la fonction
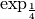 est strictement décroissante :
est strictement décroissante :
Si  , la fonction
, la fonction 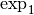 est constante :
est constante :
Si 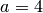 , la fonction
, la fonction 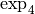 est strictement
croissante :
est strictement
croissante :
Remarque 2.2.5. Le “type de croissance” des fonctions exponentielles est différent de tous
ceux des autres fonctions que vous connaissez. Par exemple, si
 , la fonction
, la fonction 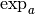 est strictement croissante
et cette croissance est de plus en plus forte au fur et à mesure que
est strictement croissante
et cette croissance est de plus en plus forte au fur et à mesure que
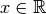 augmente. Pour passer de
augmente. Pour passer de  à
à 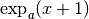 , on multiplie toujours par
, on multiplie toujours par  , ce qui
donne une croissance explosive de plus en plus rapide qui finira
toujours par dépasser celle de n’importe quelle fonction polynomiale. On
appelle ce type de croissance une croissance exponentielle (je vous
laisse deviner pourquoi).
, ce qui
donne une croissance explosive de plus en plus rapide qui finira
toujours par dépasser celle de n’importe quelle fonction polynomiale. On
appelle ce type de croissance une croissance exponentielle (je vous
laisse deviner pourquoi).
Puisque les fonctions exponentielles sont définies comme les
prolongements continus des fonctions exponentielles sur
 , on peut être certain qu’elles sont… continues :
, on peut être certain qu’elles sont… continues :
Proposition 2.2.6. Soit 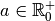 .
La fonction
.
La fonction  est continue.
est continue.
La limite en un point 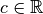 d’une fonction
exponentielle est donc toujours égale à son image en ce point. Par
ailleurs, on a :
d’une fonction
exponentielle est donc toujours égale à son image en ce point. Par
ailleurs, on a :
Proposition 2.2.7. Soit 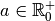 .
.
Si 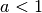 , on a
, on a  et
et 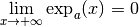 .
.
Si 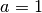 , on a
, on a 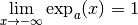 et
et 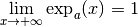 .
.
Si  , on a
, on a 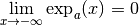 et
et 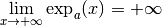 .
.
Vient à présent un des résultats les plus importants au sujet des
fonctions exponentielles. Celui-ci correspond à la bonne nouvelle selon
laquelle notre définition des fonctions exponentielles comme
prolongements continus des fonctions exponentielles sur
 permet de démontrer que les règles de calcul des
exposants que nous avions pour les exposants rationnels fonctionnent
également pour tous les exposants réels (même ceux qui ne sont pas
rationnels). C’est également cette proposition qui permet de justifier
la notation quelque peu abusive utilisée pour dénoter les images des
fonctions exponentielles.
permet de démontrer que les règles de calcul des
exposants que nous avions pour les exposants rationnels fonctionnent
également pour tous les exposants réels (même ceux qui ne sont pas
rationnels). C’est également cette proposition qui permet de justifier
la notation quelque peu abusive utilisée pour dénoter les images des
fonctions exponentielles.
Proposition 2.2.8. Soient 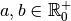 .
.
Pour tout
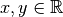 , on a :
, on a :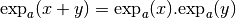

Pour tout
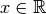 , on a :
, on a :
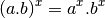
Pour tout
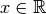 , on a :
, on a :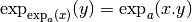
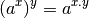
Pour tout
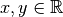 , on a :
, on a :
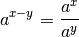
Pour tout
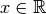 , on a :
, on a :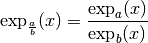
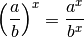
Avec cette dernière proposition, la notation pour les images des
fonctions exponentielles prend tout son sens. En effet, on sait à
présent qu’en plus de coincider avec les fonctions exponentielles sur
 , les fonctions exponentielles
, les fonctions exponentielles  (pour
(pour
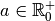 ) possèdent les mêmes propriétés
calculatoires que ces fonctions exponentielles sur
) possèdent les mêmes propriétés
calculatoires que ces fonctions exponentielles sur  .
En fait, ce sont ces propriétés qui sont fondamentales et qui
caractérisent principalement les fonctions exponentielles, en
particulier la première : les fonctions exponentielles sont des
fonctions définies sur
.
En fait, ce sont ces propriétés qui sont fondamentales et qui
caractérisent principalement les fonctions exponentielles, en
particulier la première : les fonctions exponentielles sont des
fonctions définies sur  qui transforment des sommes en
produits !
qui transforment des sommes en
produits !
2.3 La fonction exponentielle 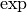 et le nombre
et le nombre  ¶
¶
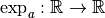 (pour
(pour
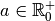 ) sont continues, mais sont-elles
dérivables ?
) sont continues, mais sont-elles
dérivables ? , la fonction
, la fonction 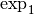 est la fonction constante
de constante
est la fonction constante
de constante  . Elle est évidemment dérivable.
. Elle est évidemment dérivable. ? Géométriquement, étant donné
les graphes de ces fonctions, nous aurions tendance à dire que oui (il
n’y a pas de cassure dans le graphe). Nous allons voir que les
fonctions exponentielles
? Géométriquement, étant donné
les graphes de ces fonctions, nous aurions tendance à dire que oui (il
n’y a pas de cassure dans le graphe). Nous allons voir que les
fonctions exponentielles 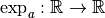 (pour
(pour 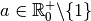 ) ont une
propriété intéressante : si elles sont dérivables en
) ont une
propriété intéressante : si elles sont dérivables en  , alors
elles sont automatiquement dérivables partout.
, alors
elles sont automatiquement dérivables partout.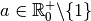 , que
signifie que la fonction
, que
signifie que la fonction 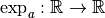 est dérivable en
est dérivable en  ? Cela signifie que la limite suivante
existe :
? Cela signifie que la limite suivante
existe :
Si cette limite existe, alors par linéarité des limites, pour tout
, les limites suivantes existent également :
Et donc la fonction
est aussi dérivable en tout
. De plus, on remarque que si la fonction
est dérivable en
, alors pour tout
on a :
Si les fonctions
sont dérivables, alors pour tout
la dérivée de
est elle-même fois une constante et cette constante est le nombre dérivée de
en
.
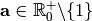 tel que :
tel que :
La fonction
sera une fonction qui est dérivable et qui est égale à sa propre dérivée ! Un tel nombre existe-t-il ? Oui : c’est le nombre dénoté habituellement par la lettre
.
Théorème 2.3.1. (Théorème du nombre e)
Il existe un unique nombre
tel que :
Ce nombre est noté
et vaut approximativement :
 a un nom spécifique et une
notation spécifique.
a un nom spécifique et une
notation spécifique.Définition 2.3.2. La fonction exponentielle (naturelle) est la fonction
 et elle est généralement
notée
et elle est généralement
notée 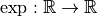 .
.
Étant donné l’existence (et l’unicité) du nombre  , nous pouvons
démontrer que la fonction exponentielle (de base
, nous pouvons
démontrer que la fonction exponentielle (de base  ) est
dérivable et égale à sa propre dérivée.
) est
dérivable et égale à sa propre dérivée.
Proposition 2.3.3. La fonction exponentielle de base  est dérivable et sa dérivée
est égale à elle-même.
est dérivable et sa dérivée
est égale à elle-même.
Soit 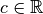 quelconque. Montrons que la fonction
quelconque. Montrons que la fonction
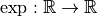 est dérivable en
est dérivable en  et
que le nombre dérivée de
et
que le nombre dérivée de 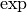 en
en  vaut
vaut  .
Il faut donc montrer que :
.
Il faut donc montrer que :
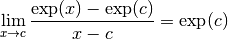
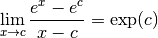
Or, par le théorème du nombre  , on sait que :
, on sait que :

On a donc :

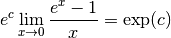
Par linéarité des limites, on a :
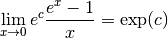
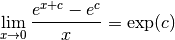
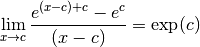
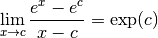
Remarque 2.3.4. C’est cette dernière proposition qui rend le nombre  aussi
incroyable : il s’agit de l’unique nombre réel strictement positif tel
que l’exponentielle ayant pour base ce nombre est dérivable et égale à
sa dérivée. Cette propriété du nombre
aussi
incroyable : il s’agit de l’unique nombre réel strictement positif tel
que l’exponentielle ayant pour base ce nombre est dérivable et égale à
sa dérivée. Cette propriété du nombre  fait qu’il possède un
statut aussi important dans les mathématiques qu’une autre constante
remarquable que vous connaissez bien :
fait qu’il possède un
statut aussi important dans les mathématiques qu’une autre constante
remarquable que vous connaissez bien : 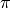 .
.
Remarque 2.3.5. La fonction exponentielle est une fonction extrêmement importante en
analyse mathématique, en particulier dans la théorie des équations
différentielles. Une équation différentielle est une équation dont la
ou les inconnues ne sont pas des nombres mais des fonctions
dérivables. L’exponentielle est l’unique solution qui vaut  en
en  à ce qui est peut-être la plus simple des équations
différentielles intéressantes :
.. math:: f=f’
Effectivement, l’exponentielle est bien une fonction égale à sa propre
dérivée.
Les équations différentielles sont extrêmement importantes en
sciences. La formalisation de la plupart des phénomènes naturels passe
par des équations différentielles.
à ce qui est peut-être la plus simple des équations
différentielles intéressantes :
.. math:: f=f’
Effectivement, l’exponentielle est bien une fonction égale à sa propre
dérivée.
Les équations différentielles sont extrêmement importantes en
sciences. La formalisation de la plupart des phénomènes naturels passe
par des équations différentielles.
Bien, nous avons donc montré que l’exponentielle de base  est
dérivable et nous nous sommes rendus compte qu’il s’agissait d’une
fonction dérivable égale à sa propre dérivée. Qu’en est-il des autres
fonctions exponentielles ? Pour le savoir, nous allons d’abord devoir
parler des logarithmes qui sont les fonctions réciproques des fonctions
exponentielles. Néanmoins, chaque chose en son temps : entraînons-nous
d’abord à manipuler nos nouvelles fonctions de référence, les fonctions
exponentielles.
est
dérivable et nous nous sommes rendus compte qu’il s’agissait d’une
fonction dérivable égale à sa propre dérivée. Qu’en est-il des autres
fonctions exponentielles ? Pour le savoir, nous allons d’abord devoir
parler des logarithmes qui sont les fonctions réciproques des fonctions
exponentielles. Néanmoins, chaque chose en son temps : entraînons-nous
d’abord à manipuler nos nouvelles fonctions de référence, les fonctions
exponentielles.
2.4 Exercices¶
Exercice 2.4.1. En utilisant les propriétés élémentaires des fonctions exponentielles, calculer les nombres suivants sans avoir recours à une calculatrice.




Exercice 2.4.2. Donner les domaines de définition réels maximaux pour les fonctions dont les expressions sont les suivantes :




Exercice 2.4.3. En utilisant les règles de transformations des graphes et les propriétés des fonctions exponentielles, tracer les graphes des fonctions suivantes.




Exercice 2.4.4 Pour les fonctions suivantes, déterminer si elles convergent ou
divergent pour 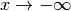 et
et 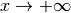 .
.








Exercice 2.4.5. Calculer les dérivées des fonctions dérivables suivantes.








Exercice 2.4.6. Donner l’équation cartésienne de la tangente au graphe de la fonction
 donnée ci-dessous au point d’abscisse
donnée ci-dessous au point d’abscisse  .
.
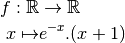

Exercice 2.4.7. et Exercice 2.4.8.

Exercice 2.4.9. La fonction suivante possède-t-elle un maximum ? Si oui, quel est-il et quel est le point de maximum associé ?
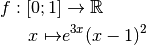

Exercice 2.4.10. Donner une primitive de la fonction exponentielle.
Solution. La fonction exponentielle.
Exercice 2.4.11. Calculer les intégrales des fonctions intégrables suivantes.