2.4 Grands théorèmes des fonctions continues (optionnel)¶
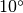 à minuit et
qu’elle est de
à minuit et
qu’elle est de 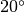 à midi et qu’on choisit une
température en
à midi et qu’on choisit une
température en 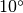 et
et 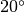 , par exemple
, par exemple
 , on est intuitivement convaincu qu’il y a eu au
moins un court instant dans la matinée où la température de la pièce
était de
, on est intuitivement convaincu qu’il y a eu au
moins un court instant dans la matinée où la température de la pièce
était de  (puisque le phénomène est continu, on doit
bien passer par toutes les valeurs intermédiaires entre
(puisque le phénomène est continu, on doit
bien passer par toutes les valeurs intermédiaires entre
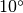 et
et 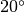 pour passer de
pour passer de
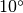 à
à 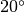 ). Cette intuition est
formalisée par le théorème suivant :
). Cette intuition est
formalisée par le théorème suivant :Théorème 2.4.1 (Théorème des valeurs intermédiaires). Soit 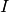 un intervalle de la forme
un intervalle de la forme 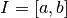 . Soit
. Soit
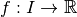 une fonction continue.
Pour tout
une fonction continue.
Pour tout 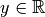 compris entre
compris entre 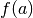 et
et
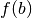 , il existe
, il existe 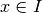 tel que
tel que 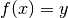 .
.
Démonstration Pas en math 4. 2
Exemple 2.4.2. Considérons la fonction suivante qui est la restriction de la fonction
carrée sur 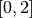 .
.
Puisque cette fonction est continue, 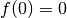 ,
, 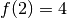 et
et
 , on peut être certain qu’il existe une abscisse
, on peut être certain qu’il existe une abscisse
 entre
entre  et
et 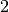 telle que la valeur de cette
fonction en
telle que la valeur de cette
fonction en  vaut exactement
vaut exactement 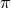 (dans ce cas-ci, il
est possible de déterminer ce
(dans ce cas-ci, il
est possible de déterminer ce  (qui est ici unique) :
(qui est ici unique) :
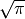 ).
).
Remarque 2.4.3. Le théorème n’affirme pas que l’abscisse  telle que
telle que
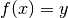 est unique ! Comme le montre l’exemple suivant (où on
choisit pour
est unique ! Comme le montre l’exemple suivant (où on
choisit pour 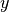 l’ordonnée
l’ordonnée  , qui se trouve entre
, qui se trouve entre
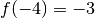 et
et 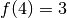 ), il peut y avoir plusieurs abscisses
de cette sorte :
), il peut y avoir plusieurs abscisses
de cette sorte :
La fonction vaut  en
en 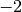 , en
, en  et en
et en 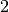 .
.
Théorème 2.4.4. Soit 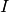 un intervalle de la forme
un intervalle de la forme 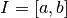 . Soit
. Soit
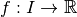 une fonction continue.
une fonction continue.
 est nécessairement bornée et atteint ses bornes, autrement
dit
est nécessairement bornée et atteint ses bornes, autrement
dit  a un point de minimum et un point de maximum.
a un point de minimum et un point de maximum.
Démonstration Pas en math 4. 3
Remarque 2.4.5. Dans le prochain chapitre, nous nous intéresserons beaucoup aux (points de) minimum et maximum d’une fonction. Ce théorème des bornes atteintes nous dit que pour une fonction continue définie sur un intervalle fermé, nous pouvons être certain qu’un point de minimum et qu’un point de maximum existe, mais il ne nous dit pas comment les trouver.
Remarque 2.4.6. La fonction dont le graphe est ci-dessous est définie sur un intervalle
de la forme 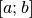 et est continue :
et est continue :
Il s’agit de la fonction :

Nous serions bien incapables (à ce stade) de déterminer quel est le (point de) maximum et le (point de) minimum de cette fonction, mais nous sommes certains que ceux-ci existent bel et bien (visuellement, on les identifie immédiatement sans pour autant être capable de les déterminer exactement).