3.2 Lien entre la continuité et les limites de fonctions

Dans la section précédente, nous avons pu observer que dans certains cas, la limite d’une fonction en un point où cette fonction est définie existe et est simplement égale à la valeur de la fonction en ce point. Dans tous les cas observés, la fonction était justement définie et continue en ce point. Il ne s’agit pas d’un hasard.

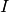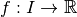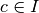Théorème 3.2.1. Soit un intervalle . Soit . Soit . Alors est continue en si et seulement si a une limite en et .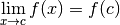

Malheureusement, la démonstration de ce théorème sort du cadre de ce cours.

Remarque 3.2.2. Il est vraiment dommage que nous ne puissions pas nous attarder sur la démonstration de ce théorème. En effet, celui-ci permet de relier la continuité aux limites, dont les définitions se ressemblent. Cette ressemblance n’est pas anodine : historiquement, ces deux notions ont été développées parallèlement et les mêmes idées ont été utilisées de part et d’autre pour arriver aux définitions actuelles.

Nous pouvons néanmoins expliquer brièvement la démonstration du théorème à partir de nos intuitions. Si une fonction est continue en un point, cela correspond au fait que son graphe ne possède pas de saut vertical en ce point, autrement dit que je peux approcher autant que je le souhaite la valeur de cette fonction en ce point à condition d’être assez proche de ce point. On retrouve assez directement l’intuition de limite : si les abscisses du graphe de la fonction se rapprochent du point considéré, les ordonnées se rapprochent donc nécessairement de l’image de ce point par la fonction, autrement dit la limite de la fonction en ce point est égale à l’image de la fonction en ce point. L’autre sens de la démonstration est tout aussi intuitif.

Avec ce théorème, nous pouvons calculer des limites de certaines fonctions sans pour autant pouvoir/devoir réaliser leurs graphes ! Donnons immédiatement un exemple.

Exemple 3.2.3. Soit la fonction

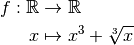
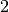Supposons qu’on souhaite calculer la limite de cette fonction en . Cette fonction est continue car c’est la somme de deux fonctions de référence (la fonction cubique et la fonction racine cubique) qui sont continues. Par le théorème 3.2.1, puisque est bien définie et continue en , on peut donc affirmer que la limite 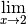existe et vaut .

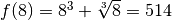Exercice 3.2.4. Calculer les limites suivantes et justifier.