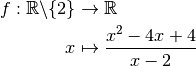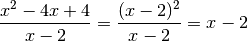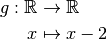3.3 Lien entre les prolongements continus et les limites de fonctions¶
Dans la section précédente, nous avons vu que calculer la limite d’une fonction en un point où elle est définie et continue est on ne peut plus simple. Mais qu’en est-il si on veut calculer la limite d’une fonction en un point où elle n’est pas définie ? Commençons avec un exemple.
Exemple 3.3.1.
Considérons la fonction :
Cette fonction n’est pas définie en
mais on pourrait se demander si elle possède malgré tout une limite en
. Malheureusement, nous ne pouvons pas invoquer le théorème 3.2.1 pour cette éventuelle limite puisque bien que la fonction soit continue partout sur son domaine de définition, elle n’est pas définie en
. Si nous pouvions trouver un prolongement continu de cette fonction défini en
, nous pourrions aisément calculer cette limite en appliquant le théorème 3.2.1. En fait, l’existence de ce prolongement continu correspond précisément à l’existence de la limite que nous recherchons et la valeur de cet éventuel prolongement continu en
est précisément la valeur de la limite recherchée ? Dès lors, comment déterminer si la fonction
possède un prolongement continu en
? Pour ce faire, jouons un peu avec l’expression de
et simplifions. Pour tout
:
Pour tout
, nous avons donc
. Attention néanmoins : cette égalité est valable seulement si
. Elle n’a pas de sens si
.
Malgré cela, remarquons que l’expression
fait sens même si
:
. Autrement dit, si on pose :
La fonction
est définie partout même en
, est continue (y compris en
) et est telle que pour tout
:
. Il s’agit d’un prolongement continu de
!
Pour la fonction
, nous pouvons appliquer le théorème 3.2.1 :
. Or, comme pour tout
:
, on a donc :
En conclusion, la limite que nous recherchions existe et vaut
.
Dans l’exemple ci-dessus, nous avons relié l’existence d’une limite en un point où une fonction n’était pas définie à l’existence d’un prolongement continu de cette fonction en ce point. Nous avons vu qu’un tel prolongement continu existait et que sa valeur au point où la fonction initiale n’était pas définie correspondant précisément à la valeur recherchée. Ce n’est pas un hasard :
Théorème 3.3.2. Soit un intervalle  . Soit
. Soit 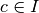 . Soit
. Soit 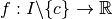 .
.
Alors
admet une limite en
si et seulement si
admet un prolongement continu en
. De plus, si la valeur de cette éventuelle limite est égale à l’image de cet éventuel prolongement continu en
.
Une fois de plus, nous ne pouvons malheureusement pas démontrer ce théorème dans ce cours. Mais à ce stade, celui-ci ne devrait pas vous surprendre. En effet, la notion de limite est précisément l’outil dont nous avions besoin pour répondre aux trois questions finales de la section 2.5. Grâce au théorème 3.3.2, nous pouvons à présent calculer des limites un peu moins triviales que celles que nous avons calculées dans la section précédente. En effet, lorsqu’on souhaite calculer la limite d’une fonction en un point où elle n’est pas défini, il suffit donc de rechercher un prolongement continu de cette fonction, ce qui peut se faire en manipulant et en simplifiant son expression.
Exercice 3.3.3. Les limites suivantes existent. Calculer celles-ci.








Remarque 3.3.4. Certaines personnes (pour être honnête : de nombreuses personnes) peu rigoureuses appliquent parfois la conclusion du théorème 3.2.1 même dans des cas où cette application n’est pas légitime, par exemple quand la fonction dont ils veulent calculer la limite n’est pas définie au point où ils veulent déterminer l’éventuelle limite. Pour donner un exemple précis, ces personnes écrivent :
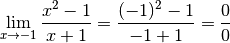
Ces personnes appellent alors ce genre de situation une indétermination .
Je vous interdis de faire de même dans ce cours.
Ce type de pratique est non rigoureuse et illogique (on applique un théorème alors que les hypothèses de ce théorème ne sont pas respectées), dangereuse (cela nuit à la compréhension de l’idée de limite (et d’infini) et fait écrire des suites de symboles qui n’ont pas de sens) et inutile (de nombreux mathématiciens dans le monde calculent des limites très efficacement sans avoir besoin d’écrire de telles horreurs). Plutôt que de ne pas réfléchir et d’écrire de façon automatique des choses qui n’ont pas de sens, prenez toujours le temps de vérifier si les hypothèses des résultats que vous souhaitez invoquer sont vérifiées et d’être certain de comprendre ce que vous êtes en train de faire.