3.4 Divergence de fonctions en un point¶
Exemple 3.4.1. Considérons la fonction :
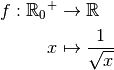
dont voici le graphe :
Que se passe-t-il quand les  se rapprochent de
se rapprochent de  ? Les
? Les
 ne se rapprochent certainement pas d’un nombre réel ! Si on
teste avec certaines valeurs de
ne se rapprochent certainement pas d’un nombre réel ! Si on
teste avec certaines valeurs de  qui se rapprochent de
qui se rapprochent de
 , on constate immédiatement que les
, on constate immédiatement que les  deviennent de
plus en plus grands :
deviennent de
plus en plus grands :
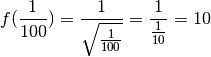

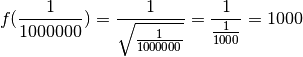
On remarque même qu’à condition de se rapprocher suffisament de
 , les valeurs de la fonction deviendront aussi grandes que l’on
veut. Autrement dit, on peut se donner n’importe quelle borne
supérieure, les valeurs
, les valeurs de la fonction deviendront aussi grandes que l’on
veut. Autrement dit, on peut se donner n’importe quelle borne
supérieure, les valeurs  de cette fonction dépassent par le
haut cette borne supérieure de façon uniforme et définitive à condition
de choisir des
de cette fonction dépassent par le
haut cette borne supérieure de façon uniforme et définitive à condition
de choisir des  suffisament proche de
suffisament proche de  . Ce
comportement est appelé divergence (vers
. Ce
comportement est appelé divergence (vers  ) et nous venons
d’en donner la définition intuitive.
) et nous venons
d’en donner la définition intuitive.
Donnons à présent la définition rigoureuse de divergence (vers
 ).
).
Définition 3.4.2. Soit un intervalle 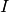 éventuellement privé d’un point
éventuellement privé d’un point  . Soit
. Soit 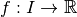 .
.
On dit que
diverge (vers
) en
si pour toute borne supérieure
, il existe
tel que pour tout
qui est à une distance plus petite ou égale de
que
, c’est-à-dire tel que
, on a nécessairement que
est plus grand ou égal à
, c’est-à-dire que
. Dans ce cas, on note :
Remarque 3.4.3. Attention : cette remarque est extrêmement importante.
Lorsqu’une fonction diverge (vers
) en un point, elle n’a pas de limite en ce point. Diverger vers
ne signifie pas se rapprocher d’un nombre appelé
(
n’est pas un nombre réel). On utilise pourtant la même notation pour parler de limite et de divergence : cela est extrêmement malheureux et absolument pas pédagogique. Cette notation étant néanmoins utilisée par tous, nous l’utiliserons également.
 ne se
lit pas la fonction
ne se
lit pas la fonction  a comme limite/converge vers
a comme limite/converge vers
 en
en  mais bien la fonction
mais bien la fonction  diverge
vers
diverge
vers  en
en  . La convergence (avoir une limite)
et la divergence sont deux notions complétement différentes.
. La convergence (avoir une limite)
et la divergence sont deux notions complétement différentes.Exemple 3.4.4. La fonction
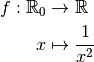
dont le graphe est :
diverge vers  en
en  . On note :
. On note :
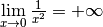 .
.
Il existe un autre phénomène possible lorsqu’une fonction ne converge
pas en un point, très semblable à la divergence vers  :
il s’agit de la divergence vers
:
il s’agit de la divergence vers  . Pour l’introduire,
commençons avec un exemple.
. Pour l’introduire,
commençons avec un exemple.
Exemple 3.4.5. Considérons la fonction

dont le graphe est :
Que se passe-t-il quand les  se rapprochent de
se rapprochent de  ? À
nouveau, les
? À
nouveau, les  ne se rapprochent certainement pas d’un nombre
réel ! Si on teste avec certaines valeurs de
ne se rapprochent certainement pas d’un nombre
réel ! Si on teste avec certaines valeurs de  qui se
rapprochent de
qui se
rapprochent de  , on constate immédiatement que les
, on constate immédiatement que les  deviennent de plus en plus grands négativement :
deviennent de plus en plus grands négativement :
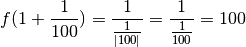



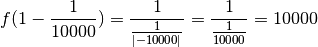

On remarque même qu’à condition de se rapprocher suffisament de
 , les valeurs de la fonction deviendront aussi grandes
négativement que l’on veut. Autrement dit, on peut se donner n’importe
quelle borne inférieure, les valeurs
, les valeurs de la fonction deviendront aussi grandes
négativement que l’on veut. Autrement dit, on peut se donner n’importe
quelle borne inférieure, les valeurs  de cette fonction
dépassent par le bas cette borne supérieure de façon uniforme et
définitive à condition de choisir des
de cette fonction
dépassent par le bas cette borne supérieure de façon uniforme et
définitive à condition de choisir des  suffisament proche de
suffisament proche de
 . Ce comportement est appelé divergence (vers
. Ce comportement est appelé divergence (vers  )
et nous venons d’en donner la définition intuitive.
)
et nous venons d’en donner la définition intuitive.
Donnons à présent la définition rigoureuse de divergence (vers
 ).
).
Définition 3.4.6. Soit un intervalle 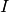 éventuellement privé d’un point
éventuellement privé d’un point  . Soit
. Soit 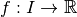 .
.
On dit que
diverge (vers
) en
si pour toute borne supérieure
, il existe
tel que pour tout
qui est à une distance plus petite ou égale de
que
, c’est-à-dire tel que
, on a nécessairement que
est plus grand ou égal à
, c’est-à-dire tel que
. Dans ce cas, on note :
Remarque 3.4.7. Même remarque que pour la divergence vers  : diverger
vers
: diverger
vers  ne signifie pas avoir comme limite un nombre
appelé
ne signifie pas avoir comme limite un nombre
appelé  .
.
Exemple 3.4.8. La fonction

dont le graphe est :
diverge vers  en
en 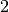 . On note :
. On note :
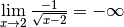 .
.
 et divergence
et divergence sont mutuellement exclusives. En effet :
sont mutuellement exclusives. En effet :- Si une fonction converge (a une limite) en un point, ses valeurs ne peuvent pas devenir arbitrairement grandes (que ce soit positivement ou négativement) puisque qu’elle se rapproche de la limite (qui est un nombre réel).
Si une fonction diverge vers
 en un point, ses valeurs
ne peuvent se rapprocher d’un nombre réel (puisque celles-ci
deviennent de plus en plus grandes positivement au fur et à mesure
qu’on se rapproche du point où la fonction diverge) et ne peuvent
devenir arbitrairement grandes négativement (puisque celles-ci
deviennent de plus en plus grandes positivement au fur et à
mesure qu’on se rapproche du point où la fonction diverge).
en un point, ses valeurs
ne peuvent se rapprocher d’un nombre réel (puisque celles-ci
deviennent de plus en plus grandes positivement au fur et à mesure
qu’on se rapproche du point où la fonction diverge) et ne peuvent
devenir arbitrairement grandes négativement (puisque celles-ci
deviennent de plus en plus grandes positivement au fur et à
mesure qu’on se rapproche du point où la fonction diverge).Si une fonction diverge vers
 en un point, ses valeurs
ne peuvent se rapprocher d’un nombre réel (puisque celles-ci
deviennent de plus en plus grandes négativement au fur et à mesure
qu’on se rapproche du point où la fonction diverge) et ne peuvent
devenir arbitrairement grandes négativement (puisque celles-ci
deviennent de plus en plus grandes négativement au fur et à
mesure qu’on se rapproche du point où la fonction diverge).
en un point, ses valeurs
ne peuvent se rapprocher d’un nombre réel (puisque celles-ci
deviennent de plus en plus grandes négativement au fur et à mesure
qu’on se rapproche du point où la fonction diverge) et ne peuvent
devenir arbitrairement grandes négativement (puisque celles-ci
deviennent de plus en plus grandes négativement au fur et à
mesure qu’on se rapproche du point où la fonction diverge).
Proposition 3.4.9. Soit un intervalle 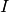 éventuellement privé d’un point
éventuellement privé d’un point  . Soit
. Soit 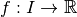 .
.
Si
 possède une limite en
possède une limite en  , alors
, alors  ne
diverge pas vers
ne
diverge pas vers  en
en  et ne diverge pas vers
et ne diverge pas vers
 en
en  .
.Si
 diverge vers
diverge vers  en
en  , alors
, alors
 ne possède pas une limite en
ne possède pas une limite en  et ne diverge pas
vers
et ne diverge pas
vers  en
en  .
.Si
 diverge vers
diverge vers  en
en  , alors
, alors
 ne possède pas une limite en
ne possède pas une limite en  et ne diverge pas
vers
et ne diverge pas
vers  en
en  .
.
 et de
divergence vers
et de
divergence vers  , donnons quelques exemples et
contre-exemples supplémentaires.
, donnons quelques exemples et
contre-exemples supplémentaires.Contre-exemple 3.4.10. Les seules fonctions de référence qui ne sont pas définies sur tout 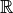 sont la fonction racine carrée et la fonction
inverse. Nous savons déjà que la fonction racine carrée a comme limite
sont la fonction racine carrée et la fonction
inverse. Nous savons déjà que la fonction racine carrée a comme limite
 lorsque
lorsque  tend vers
tend vers  , mais qu’en est-il de
la fonction inverse ? Diverge-t-elle ?
Rappelons que la fonction inverse est la fonction :
, mais qu’en est-il de
la fonction inverse ? Diverge-t-elle ?
Rappelons que la fonction inverse est la fonction :
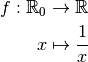
Son graphe est le suivant.
Lorsque les 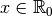 se rapprochent de
se rapprochent de  ,
les nombres
,
les nombres 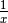 ne se rapprochent certainement pas d’un
nombre de manière uniforme et définitive. Mais ils ne deviennent pas non
plus arbitrairement grands positivement de manière uniforme et
définitive (ils le deviennt à droite de
ne se rapprochent certainement pas d’un
nombre de manière uniforme et définitive. Mais ils ne deviennent pas non
plus arbitrairement grands positivement de manière uniforme et
définitive (ils le deviennt à droite de  , mais pas à gauche )
et ils ne deviennent pas non plus arbitrairement grands négativement de
manière uniforme et définitive (ils le deviennt à gauche de
, mais pas à gauche )
et ils ne deviennent pas non plus arbitrairement grands négativement de
manière uniforme et définitive (ils le deviennt à gauche de  ,
mais pas à droite ). En conclusion, la fonction inverse n’a pas de
limite en
,
mais pas à droite ). En conclusion, la fonction inverse n’a pas de
limite en  , mais ne diverge pas non plus en
, mais ne diverge pas non plus en  (que ce
soit vers
(que ce
soit vers  ou vers
ou vers  ).
).
Remarque 3.4.11. La fonction inverse ne diverge pas vers  ou vers
ou vers
 en
en  , mais par contre son produit avec elle-même
diverge vers
, mais par contre son produit avec elle-même
diverge vers  en
en  : voir exemple
3.4.4.
: voir exemple
3.4.4.
Exemple 3.4.12. La fonction 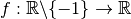 dont
le graphe est le suivant :
dont
le graphe est le suivant :
diverge vers  en
en 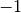 . On note :
. On note :
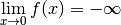 .
.
Exemple 3.4.13. La fonction  dont le graphe est le
suivant :
dont le graphe est le
suivant :
diverge vers  en
en  (même si la fonction est
définie en
(même si la fonction est
définie en  de telle sorte que
de telle sorte que  ). On note :
). On note :
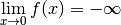 .
.
Contre-exemple 3.4.14. La fonction 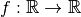 dont le graphe est le
suivant :
dont le graphe est le
suivant :
ne converge pas et ne diverge pas en 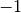 .
.
Contre-exemple 3.4.15. La fonction  dont
le graphe est le suivant :
dont
le graphe est le suivant :
ne converge pas et ne diverge pas en  .
.
À présent, exerçons-nous un peu.
Exercice 3.4.16. À l’aide d’un graphique, déterminer si les fonctions divergent au point
considéré. Si oui, donner le type de divergence (vers  ou
vers
ou
vers  ).
).




Exercice 3.4.17. Voici le graphe d’une fonction réelle  . Déterminer l’ensemble
des points où elle diverge.
. Déterminer l’ensemble
des points où elle diverge.

Exercice 3.4.18. Tracer le graphe d’une fonction  définie sur
définie sur
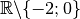 qui diverge vers
qui diverge vers  en
en 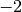 et qui ne diverge et ne converge pas en
et qui ne diverge et ne converge pas en  .
.
Solution.
Exercice 3.4.19. Déterminer si les fonctions dont les graphes sont donnés ci-dessous divergent aux points indiqués.
Solution.
|
|
Exercice 3.4.20 Tracer le graphe d’une fonction  ayant les propriétés suivantes
:
ayant les propriétés suivantes
:
Solution.
Exercice 3.4.21 Tracer le graphe d’une fonction
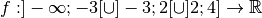 qui est
continue partout sauf en
qui est
continue partout sauf en 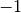 et
et  , qui a comme limite
, qui a comme limite
 en
en 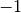 et comme limite
et comme limite  en
en
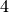 , qui n’a pas de limite en
, qui n’a pas de limite en  , qui diverge vers
, qui diverge vers
 en -3 et qui ne diverge pas en
en -3 et qui ne diverge pas en 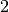 .
.
Solution.
Exercice 3.4.22 Déterminer si les fonctions convergent ou divergent au point considéré.
Si elles convergent, donner la limite. Si elles divergent, donner le
type de divergence (vers  ou vers
ou vers  ).
).










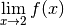

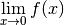
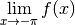


 .
. .
.