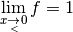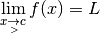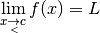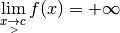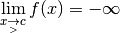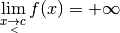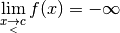3.5 Limites à gauche et limites à droite¶
Exemple 3.5.1. La fonction  dont le graphe est :
dont le graphe est :
 . Lorsque les abscisses se rapprochent
de
. Lorsque les abscisses se rapprochent
de  , les points du graphe de
, les points du graphe de  ne se rapprochent pas
définitivement et uniformément d’une seule valeur.
ne se rapprochent pas
définitivement et uniformément d’une seule valeur. , la fonction réduite
, la fonction réduite
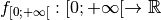 possède bien une
limite en
possède bien une
limite en  :
:On a : 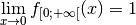 . De même,
si nous ne considérons que les points du graphe dont les abscisses sont
inférieures à
. De même,
si nous ne considérons que les points du graphe dont les abscisses sont
inférieures à  , la fonction réduite
, la fonction réduite
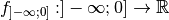 possède bien une
limite en
possède bien une
limite en  :
:
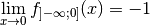 .
.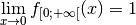 ,
cela signifie précisément que la fonction
,
cela signifie précisément que la fonction  possède une limite
à droite de 0 et que celle-ci vaut
possède une limite
à droite de 0 et que celle-ci vaut  , ce qu’on note :
, ce qu’on note :
Lorsqu’on affirme que
, cela signifie précisément que la fonction
possède une limite à gauche de 0 et que celle-ci vaut
, ce qu’on note :
Donnons à présent la définition générale de limite à droite et de limite à gauche : il s’agit simplement d’utiliser la définition de limite et de restriction de fonction.
Définition 3.5.2. Soit un intervalle  éventuellement privé d’un point
éventuellement privé d’un point  . Soit
. Soit  .
.
On dit que
a une limite à droite
en
si la fonction
a comme limite
en
. On note :
On dit que
a une limite à gauche
en
si la fonction
a comme limite
en
. On note :
Remarque 3.5.3. Certaines personnes préfèrent utiliser les notations
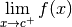 pour les limites à droite et
pour les limites à droite et
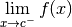 pour les limites à gauche. Je
vous déconseille d’utiliser ces notations.
pour les limites à gauche. Je
vous déconseille d’utiliser ces notations.
Donnons quelques exemples et contre-exemples.
Exemple 3.5.4. La fonction  dont le graphe est :
dont le graphe est :
 qui vaut
qui vaut  :
:
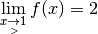 .
. .
.Exemple 3.5.5. La fonction carrée  dont le graphe
est :
dont le graphe
est :
 qui vaut
qui vaut 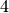 :
:
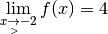 .
. a aussi une limite à gauche en
a aussi une limite à gauche en  qui
vaut aussi
qui
vaut aussi 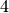 :
:
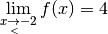 .
.Contre-exemple 3.5.6. La fonction inverse  dont le graphe
est :
dont le graphe
est :
n’a pas de limite à droite en  et n’a pas de limite à gauche en
et n’a pas de limite à gauche en
 .
.
Dans tous les exemples déjà rencontrés, remarquons que le seul où la fonction admet une limite à droite et une limite à gauche au point considéré et que ces deux limites sont égales correspond au cas où la fonction admet une (véritable) limite en ce point, qui est d’ailleurs égale à l’unique valeur de la limite à droite et de la limite à gauche.
Ce n’est pas un hasard : pour avoir une limite en un point  ,
une fonction
,
une fonction  doit se rapprocher de façon définitive et
uniforme d’une unique valeur, elle doit donc avoir une limite à gauche
en ce point et une limite à droite en ce point et celles-ci doivent être
identiques. L’inverse est vrai aussi : si une fonction
doit se rapprocher de façon définitive et
uniforme d’une unique valeur, elle doit donc avoir une limite à gauche
en ce point et une limite à droite en ce point et celles-ci doivent être
identiques. L’inverse est vrai aussi : si une fonction  a une
limite à gauche en un point
a une
limite à gauche en un point  et une limite à droite en
et une limite à droite en
 et que celles-ci sont égales, alors
et que celles-ci sont égales, alors  se rapprochent
bien définitivement et uniformément de cet unique nombre au fur et à
mesure qu’on se rapproche de
se rapprochent
bien définitivement et uniformément de cet unique nombre au fur et à
mesure qu’on se rapproche de  ! Plus rigoureusement, on peut
démontrer :
! Plus rigoureusement, on peut
démontrer :
Proposition 3.5.7. Soit un intervalle  éventuellement privé d’un point
éventuellement privé d’un point  . Soit
. Soit  .
.
Alors
possède une limite
en
si et seulement si
possède une limite à droite
en
et une limite à gauche
en
et que celles-ci sont égales :
.
Remarque 3.5.8. Certaines personnes aiment beaucoup les limites à droite et les limites à gauche, à tel point qu’elles définissent celles-ci en premier et les utilisent pour définir la notion de limite générale.
Pourtant, c’est bien la notion de limite qui est fondamentale, si utile et qui permet de démontrer d’impressionnants résultats mathématiques. De plus, les notions de limite à droite et limite à gauche ne se généralisent pas lorsqu’on ne peut pas parler de droite et de gauche tandis que la notion de limite plus gobale se généralise dans de nombreux contextes.
Pour ces raisons, nous n’insisterons volontairement pas sur les notions de limites à droite et de limite à gauche dans ce cours.
Exemple 3.5.9. Considérons la fonction inverse
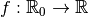 dont le graphe est :
dont le graphe est :
Comme nous l’avons vu dans la section précédente, cette fonction ne
diverge pas (que ce soit vers  ou
ou  en
en
 ). Par contre, si nous ne considérons que les points de son
domaine qui sont plus grands ou égaux à
). Par contre, si nous ne considérons que les points de son
domaine qui sont plus grands ou égaux à  , on obtient la
fonction
, on obtient la
fonction 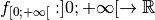 dont le
graphe est :
dont le
graphe est :
 en
en  :
:
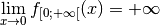 .
. , on obtient
la fonction
, on obtient
la fonction
 dont
le graphe est :
dont
le graphe est : en
en  :
:
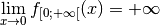 .
. diverge vers
diverge vers  à droite de
à droite de
 , ce qu’on note
, ce qu’on note
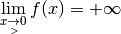 et qu’elle
diverge vers
et qu’elle
diverge vers  à gauche de
à gauche de  , ce qu’on note
, ce qu’on note
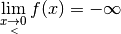 .
.Définition 3.5.10. Soit un intervalle  éventuellement privé d’un point
éventuellement privé d’un point  . Soit
. Soit  .
.
On dit que
diverge vers :math:`+infty` à droite en
si la fonction
diverge vers
en
. On note :
On dit que
diverge vers :math:`-infty` à droite en
si la fonction
diverge vers
en
. On note :
On dit que
a diverge vers :math:`+infty` à gauche en
si la fonction
diverge vers
en
. On note :
On dit que
a diverge vers :math:`-infty` à gauche en
si la fonction
diverge vers
en
. On note :
On a un résultat équivalent pour les divergence à gauche et à droite à celui qu’on avait pour les limites :
Proposition 3.5.11. Soit un intervalle  éventuellement privé d’un point
éventuellement privé d’un point  . Soit
. Soit  .
.
Alors
diverge vers
en
si et seulement si
diverge vers
à droite en
et
diverge vers
à gauche en
.
De plus,
diverge vers
en
si et seulement si
diverge vers
à droite en
et
diverge vers
à gauche en
.
Exemple 3.5.12. La fonction  dont le graphe est :
dont le graphe est :
diverge vers  à droite en
à droite en  et diverge vers
et diverge vers
 à gauche en
à gauche en  . Elle diverge vers
. Elle diverge vers  en
en  .
.
Exemple 3.5.13. La fonction  dont le graphe est :
dont le graphe est :
diverge vers  à gauche en
à gauche en  . Elle ne diverge pas
à droite en
. Elle ne diverge pas
à droite en  .
.
Exemple 3.5.14. La fonction carrée  dont le graphe
est :
dont le graphe
est :
ne diverge ni à gauche ni à droite en  .
.
Exercice 3.5.15. Pour la fonction dont le graphe est ci-dessous, quels sont les points où la fonction a une limite à gauche ou à droite mais n’a pas de limite ? Quels sont les points où la fonction diverge à gauche ou à droite mais ne diverge pas ? Pour tous ces points, donner les limites ou les divergences à gauche ou à droite éventuelles.
Solution. Le seul point où la fonction n’a pas de limite ou ne diverge pas est
 . La fonction a une limite à gauche en
. La fonction a une limite à gauche en  qui vaut
qui vaut
 et diverge vers
et diverge vers  à droite en
à droite en  .
.
Exercice 3.5.16. Tracer le graphe d’une fonction  ayant les propriétés suivantes
:
ayant les propriétés suivantes
:
Solution.
Exemple 3.5.17. Déterminer quelles sont les limites et les divergence à gauche et à droite.





Exercice 3.5.18. Tracer le graphe d’une fonction
 qui est
continue partout sauf en
qui est
continue partout sauf en  et
et  , qui vaut
, qui vaut  en
en
 ,
, 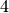 en
en  et
et 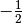 en
en 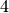 ,
qui a comme limite à gauche
,
qui a comme limite à gauche  en
en  et comme limite à
droite
et comme limite à
droite  en
en  , qui a comme limite à gauche
, qui a comme limite à gauche  en
en  et qui diverge vers
et qui diverge vers  à droite en
à droite en  ,
qui diverge vers
,
qui diverge vers  à gauche en
à gauche en  et qui diverge
vers
et qui diverge
vers  à droite en
à droite en  .
.
Solution.
Exercice 3.5.19. Déterminer si les fonctions convergent ou divergent à droite ou à gauche
au point considéré. Si elles convergent à droite ou à gauche, donner la
limite à droite ou à gauche. Si elles divergent à droite ou à gauche,
donner le type de divergence (vers  ou vers
ou vers
 ). N’hésitez pas à vous aider d’un graphe.
). N’hésitez pas à vous aider d’un graphe.