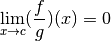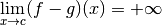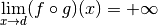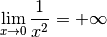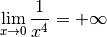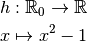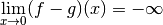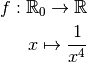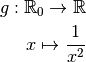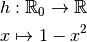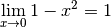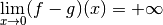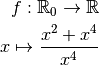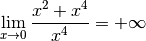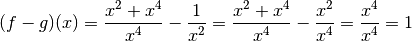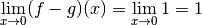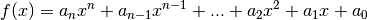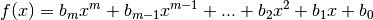3.8 Propriétés des limites de fonctions¶
Exemple 3.8.1. À ce stade, nous savons déjà que la fonction inverse converge
vers  pour
pour  qui tend vers
qui tend vers  :
:
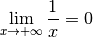
De même, nous savons que la fonction constante de constante  converge vers
converge vers  :
:

Question : à partir de ces deux informations, pouvons-nous affirmer
quelque chose au sujet du comportement asymptotique (pour  qui
tend vers
qui
tend vers  ) de la fonction obtenue en additionnant ces
deux premières fonctions :
) de la fonction obtenue en additionnant ces
deux premières fonctions :

Bien entendu, calculer directement la limite pour  qui tend
vers
qui tend
vers  de cette fonction
de cette fonction  n’est pas difficile :
n’est pas difficile :
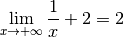
Mais aurions-nous pu trouver ce résultat sans même réfléchir au
comportement asymptotique de la fonction  ? Pour répondre à
cette question, rappelons ce que signifient les deux affirmations :
? Pour répondre à
cette question, rappelons ce que signifient les deux affirmations :
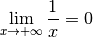

La première signifie que pour des nombres  de plus en plus
grands, les nombres
de plus en plus
grands, les nombres 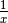 se rapprochent uniformément et
définitivement de
se rapprochent uniformément et
définitivement de  . La deuxième signifie que pour des nombres
. La deuxième signifie que pour des nombres
 de plus en plus grands, les nombres
de plus en plus grands, les nombres  se rapprochent
uniformément et définitivement de
se rapprochent
uniformément et définitivement de  . On déduit directement de
ces deux informations que pour des nombres
. On déduit directement de
ces deux informations que pour des nombres  de plus en plus
grands, les nombres
de plus en plus
grands, les nombres 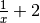 se rapprochent uniformément et
définitivement de
se rapprochent uniformément et
définitivement de 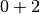 . Autrement dit :
. Autrement dit :
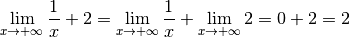
La limite pour  qui tend vers
qui tend vers  de la fonction
de la fonction
 qui est définie comme la somme de la fonction inverse et de la
fonction constante de constante
qui est définie comme la somme de la fonction inverse et de la
fonction constante de constante  est égale à la somme des
limites pour
est égale à la somme des
limites pour  qui tend vers
qui tend vers  de ces deux
fonctions. On a pu décomposer le calcul de la limite pour
de ces deux
fonctions. On a pu décomposer le calcul de la limite pour  qui
tend vers
qui
tend vers  de la fonction
de la fonction  en une somme de
limites plus simples à calculer.
en une somme de
limites plus simples à calculer.
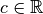 .
.Proposition 3.8.2. Soit  un intervalle éventuellement privé d’un point
un intervalle éventuellement privé d’un point  .
.
Soient
et
telles que
et
. Alors la fonction
a une limite en
et on a :
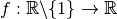 et
et
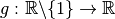 dont les graphes
sont les suivants :
dont les graphes
sont les suivants :Ces deux fonctions ont toutes les deux une limite en  :
:
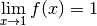
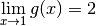
Que se passe-t-il si nous nous créons une nouvelle fonction en
additionnant  et
et  :
:
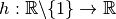 .
.
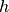 a également une limite en
a également une limite en  et cette
limite est la somme des limites en
et cette
limite est la somme des limites en  des fonctions
des fonctions  et
et  :
: 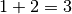 .
. se rapproche uniformément et
définitivement de
se rapproche uniformément et
définitivement de  à l’approche de
à l’approche de  et que la
fonction
et que la
fonction  se rapproche uniformément et définitivement de
se rapproche uniformément et définitivement de
 à l’approche de
à l’approche de  , la fonction
, la fonction  qui est la
somme de ces deux fonctions se rapproche uniformément et
définitivement de
qui est la
somme de ces deux fonctions se rapproche uniformément et
définitivement de 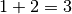 à l’approche de
à l’approche de  . Cette
remarque n’est évidemment pas propre à notre exemple : il en aurait
été de même pour d’autres fonctions
. Cette
remarque n’est évidemment pas propre à notre exemple : il en aurait
été de même pour d’autres fonctions  et
et  . C’est ce
qui est exactement exprimé par la proposition
3.8.2.
. C’est ce
qui est exactement exprimé par la proposition
3.8.2.Exemple 3.8.3. Supposons que l’on souhaite déterminer si la fonction suivante possède
une limite en  .
.
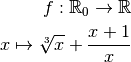
On remarque que la fonction  est la somme des trois fonctions :
est la somme des trois fonctions :
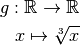
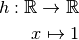
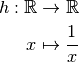
De plus, on sait facilement calculer les limites en  de ces
trois fonctions :
de ces
trois fonctions :
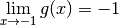
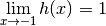

Par la proposition 3.8.2,  a donc
nécessairement une limite en
a donc
nécessairement une limite en  et cette limite est égale à :
et cette limite est égale à :
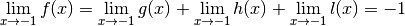
La proposition 3.8.2 décrit ce qu’il se passe lorsqu’on additionne deux fonctions qui possèdent une limite en un point. Il existe bien évidemment d’autres opérations sur les fonctions et d’autres possibilités pour une fonction que d’avoir une limite en un point (elle peut par exemple diverger). Dans les pages suivantes, nous allons donner toutes les variantes possibles de la proposition 3.8.2. Insistons sur un point : n’apprennez pas toutes ces propositions par cœur ! Comprenez-les de sorte que vous puissiez les retrouver par vous-mêmes.
Proposition 3.8.4. Soit  un intervalle éventuellement privé d’un point
un intervalle éventuellement privé d’un point  .
.
Soient
et
telles que
et
. Alors la fonction
a une limite en
et on a :
Proposition 3.8.5. Soit  un intervalle éventuellement privé d’un point
un intervalle éventuellement privé d’un point  .
.
Soient
et
telles que
et
. Alors la fonction
a une limite en
et on a :
- Proposition 3.8.6. Soit
 un intervalle éventuellement privé d’un point
un intervalle éventuellement privé d’un point  .
Soient
.
Soient  et
et  avec
avec  pour tout
pour tout 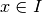 telles que
telles que
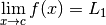 et
et
 avec
avec  .
Alors la fonction
.
Alors la fonction 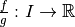 a une limite
en
a une limite
en  et on a :
et on a :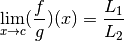
Proposition 3.8.7. Soit  un intervalle éventuellement privé d’un point
un intervalle éventuellement privé d’un point  et soit
et soit 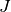 un intervalle éventuellement privé d’un point
un intervalle éventuellement privé d’un point  .
.
Soient
et
telles que
,
et
. Alors la fonction
a une limite en
et on a :
Passons aux cas où la fonction  diverge vers
diverge vers  .
.
Proposition 3.8.8. Soit  un intervalle éventuellement privé d’un point
un intervalle éventuellement privé d’un point  .
.
Soient
et
telles que
et
. Alors la fonction
diverge en
et on a :
Proposition 3.8.9. Soit  un intervalle éventuellement privé d’un point
un intervalle éventuellement privé d’un point  .
.
Soient
et
telles que
et
. Alors la fonction
diverge en
et on a :
Proposition 3.8.10. Soit  un intervalle éventuellement privé d’un point
un intervalle éventuellement privé d’un point  .
.
Soient
et
telles que
avec
et
. Alors la fonction
diverge en
et on a :
Si
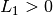 :
: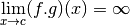
Si
 :
: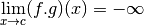
Proposition 3.8.11. Soit  un intervalle éventuellement privé d’un point
un intervalle éventuellement privé d’un point  .
.
Soient
et
avec
pour tout
telles que
et
. Alors la fonction
a une limite en
et on a :
Proposition 3.8.12. Soit  un intervalle non majoré et soit
un intervalle non majoré et soit 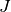 un intervalle éventuellement privé d’un point
un intervalle éventuellement privé d’un point  .
.
Soient
et
telles que
,
et
. Alors la fonction
a une limite en
et on a :
Les cas où la fonction  diverge vers
diverge vers  sont très
similaires aux cinq précédents et nous ne les listerons pas ici. Passons
aux cas où la fonction
sont très
similaires aux cinq précédents et nous ne les listerons pas ici. Passons
aux cas où la fonction  diverge vers
diverge vers  mais où la
fonction
mais où la
fonction  converge.
converge.
Proposition 3.8.13. Soit  un intervalle éventuellement privé d’un point
un intervalle éventuellement privé d’un point  .
.
Soient
et
telles que
et
. Alors la fonction
diverge en
et on a :
Proposition 3.8.14. Soit  un intervalle éventuellement privé d’un point
un intervalle éventuellement privé d’un point  .
.
Soient
et
telles que
et
. Alors la fonction
diverge en
et on a :
Proposition 3.8.15. Soit  un intervalle éventuellement privé d’un point
un intervalle éventuellement privé d’un point  .
.
Soient
et
telles que
avec
et
. Alors la fonction
diverge en
et on a :
Si
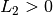 :
: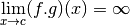
Si
 :
: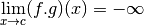
Proposition 3.8.16. Soit  un intervalle éventuellement privé d’un point
un intervalle éventuellement privé d’un point  .
.
Soient
et
avec
pour tout
telles que
et
. Alors la fonction
diverge en
et on a :
Si
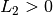 :
: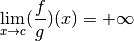
Si
 :
: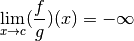
Proposition 3.8.17. Soit  un intervalle éventuellement privé d’un point
un intervalle éventuellement privé d’un point  et soit
et soit 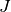 un intervalle éventuellement privé d’un point
un intervalle éventuellement privé d’un point
 .
.
Soient
et
telles que
,
et
. Alors la fonction
diverge en
et on a :
À nouveau, les cas où la fonction  diverge vers
diverge vers  sont très similaires aux cinq précédents et nous ne les listerons pas
ici. Passons aux cas où la fonction
sont très similaires aux cinq précédents et nous ne les listerons pas
ici. Passons aux cas où la fonction  diverge vers
diverge vers
 et où la fonction
et où la fonction  diverge vers
diverge vers
 .
.
Proposition 3.8.18. Soit  un intervalle éventuellement privé d’un point
un intervalle éventuellement privé d’un point
 .
.
Soient
et
telles que
et
. Alors la fonction
diverge en
et on a :
Proposition 3.8.19. Soit  un intervalle éventuellement privé d’un point
un intervalle éventuellement privé d’un point
 .
.
Soient
et
telles que
avec
et
. Alors la fonction
diverge en
et on a :
Proposition 3.8.20. Soit  un intervalle non majoré et soit
un intervalle non majoré et soit 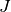 un
intervalle éventuellement privé d’un point
un
intervalle éventuellement privé d’un point  .
.
Soient
et
telles que
,
et
. Alors la fonction
diverge en
et on a :
Les cas où la fonction  ou la fonction
ou la fonction  diverge vers
diverge vers
 plutôt que vers
plutôt que vers  sont très similaires aux
cinq derniers et nous ne les listerons pas ici. Tous les cas où on ne
considère pas une limite ou une divergence en un point mais pour
sont très similaires aux
cinq derniers et nous ne les listerons pas ici. Tous les cas où on ne
considère pas une limite ou une divergence en un point mais pour
 qui tend vers
qui tend vers  ou vers
ou vers  sont
semblables à ceux que nous avons déjà listés, nous ne les listerons donc
pas ici.
sont
semblables à ceux que nous avons déjà listés, nous ne les listerons donc
pas ici.
Remarque 3.8.21. Il peut sembler que certaines propositions sont manquantes. Par
exemples, quid de la différence de deux fonctions qui divergent vers
 en un point
en un point  ?
Une personne peu rigoureuse pourrait écrire que :
?
Une personne peu rigoureuse pourrait écrire que :

Outre le fait que cela n’a aucun sens, cela est absolument faux ! Je vous interdis de noter de telles horreurs dans le cadre de ce cours.
Ce type de situation est appelé par certaines personnes indétermination . Une indétermination est en fait une situation où on ne peut pas simplement appliquer une des propositions listées ci-dessus pour décomposer une limite ou une divergence que l’on cherche à calculer. Il faut dans ces cas-là ruser, simplifier l’expression de la fonction considérée ou même être imaginatif ! Toutes sortes de choses peuvent arriver !
Illustrons cette dernière affirmation. Commençons par donner un
exemple de deux fonctions qui divergent vers  en un
point mais dont la différence ne converge pas vers
en un
point mais dont la différence ne converge pas vers  , elle
diverge vers
, elle
diverge vers  .
.
Considérons les deux fonctions :
On a :
Pour tout
, on a :
La fonction
peut être vue comme le produit des deux fonctions :
On a :
Par la proposition 3.8.10, on en déduit que :
À présent, donnons un exemple de deux fonctions qui divergent vers
en un point mais dont la différence diverge vers
. Considérons les deux fonctions :
On a :
Pour tout
, on a :
La fonction
peut être vue comme le produit des deux fonctions :
On a :
Par la proposition 3.8.10, on en déduit que :
Enfin, la différence de deux fonctions qui divergent vers
en un point peut malgré tout parfois converger (vers
ou un autre nombre). Considérons par exemple les deux fonctions :
On a :
Pour tout
, on a :
On en déduit :
Comme on peut le voir avec ces trois exemples, lorsqu’on est face à une indétermination, il n’y a pas d’autre choix que de se mettre à réfléchir. Il n’y a pas de loi générale.
 qui tend
vers
qui tend
vers  (ou vers
(ou vers  ) dans le cas d’une
fonction rationnelle (quotient de deux polynômes).
) dans le cas d’une
fonction rationnelle (quotient de deux polynômes).Théorème 3.8.22. (Théorème de la règle des plus hautes puissances)
 un intervalle non majoré.
un intervalle non majoré. et
et  avec
avec  pour tout
pour tout 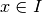 telles que pour
tout
telles que pour
tout 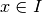 :
:
pour un certain
, un certain
et
avec
et
avec
. Alors :
- Si
,
on a :
- Si
,
on a :
- Si
pour un certain
, on a :
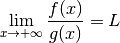
Démonstration Pour tout 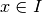 avec
avec  , on a :
, on a :

Par les propriétés des limites, on a :


De même :
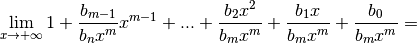
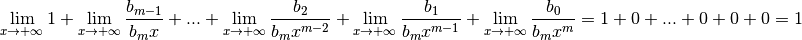
Par les propriétés des limites, on a donc :
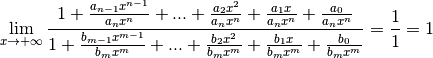
Dès lors :
Si
 ,
par les propriétés des limites et des divergences, on a :
,
par les propriétés des limites et des divergences, on a :
Si
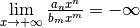 ,
par les propriétés des limites et des divergences, on a :
,
par les propriétés des limites et des divergences, on a :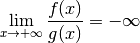
Si
 pour un certain
pour un certain  , par les propriétés des
limites, on a :
, par les propriétés des
limites, on a :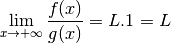
Remarque 3.8.23. Le théorème est également valable lorsqu’on considère une limite pour
 qui tend vers
qui tend vers  .
.
Exemple 3.8.24. On souhaite déterminer la limite suivante :

Le théorème de la règle des plus hautes puissances nous dit que si la limite ci-dessous existe, alors la limite que nous recherchons existe aussi et est égale à celle-ci :
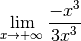
Or :
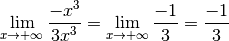
Conclusion, par le théorème de la règle des plus hautes puissances, on déduit que :

Exercice 3.8.25. Soit  un intervalle éventuellement privé d’un point
un intervalle éventuellement privé d’un point
 . Soient
. Soient  et
et
 telles que
telles que
 et
et
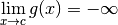 .
.
Que peut-on dire au sujet du comportement de la fonction
 au voisinage de
au voisinage de  ?
Converge-t-elle ? Diverge-t-elle ? Expliquer.
?
Converge-t-elle ? Diverge-t-elle ? Expliquer.
Solution. Puisque  , pour des nombres
, pour des nombres
 de plus en plus proches de
de plus en plus proches de  , les nombres
, les nombres  deviennent uniformément et définitivement arbitrairement grands. Puisque
deviennent uniformément et définitivement arbitrairement grands. Puisque
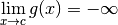 , pour des nombres
, pour des nombres  de plus en plus proches de
de plus en plus proches de  , les nombres
, les nombres 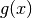 deviennent uniformément et définitivement arbitrairement petits. Dès
lors, pour des nombres
deviennent uniformément et définitivement arbitrairement petits. Dès
lors, pour des nombres  de plus en plus proches de
de plus en plus proches de  ,
les nombres
,
les nombres  deviennent uniformément et définitivement
arbitrairement petits (le produit de nombres de plus en plus grands par
des nombres petits est de plus en plus petit).
deviennent uniformément et définitivement
arbitrairement petits (le produit de nombres de plus en plus grands par
des nombres petits est de plus en plus petit).
Exercice 3.8.26. Soit  un intervalle non minoré. Soient
un intervalle non minoré. Soient
 et
et  avec
avec
 pour tout
pour tout 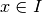 telles que
telles que
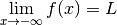 pour un certain
pour un certain
 et
et
 .
.
Que peut-on dire au sujet du comportement de la fonction
 pour
pour  qui tend vers
qui tend vers
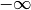 ? Converge-t-elle ? Diverge-t-elle ? Expliquer.
? Converge-t-elle ? Diverge-t-elle ? Expliquer.
Solution. Puisque 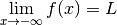 , pour des nombres
, pour des nombres
 de plus en plus petits, les nombres
de plus en plus petits, les nombres  se
rapprochent uniformément et définitivement de
se
rapprochent uniformément et définitivement de 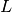 . Puisque
. Puisque
 , pour des nombres
, pour des nombres
 de plus en plus petits, les nombres
de plus en plus petits, les nombres 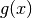 deviennent
uniformément et définitivement arbitrairement petits. Dès lors, pour des
nombres
deviennent
uniformément et définitivement arbitrairement petits. Dès lors, pour des
nombres  de plus en plus petits, les nombres
de plus en plus petits, les nombres
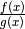 se rapprochent uniformément et définitivement
de
se rapprochent uniformément et définitivement
de  (le quotient de nombres de plus en plus proche d’un nombre
(le quotient de nombres de plus en plus proche d’un nombre
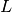 divisés par des nombres de plus en plus petits est de plus en
plus proche de
divisés par des nombres de plus en plus petits est de plus en
plus proche de  ).
).
Exercice 3.8.27. Soit  un intervalle non majoré. Soient
un intervalle non majoré. Soient
 et
et  avec
avec
 pour tout
pour tout 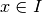 telles que
telles que
 et
et
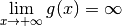 .
.
Que peut-on dire au sujet du comportement de la fonction
 pour
pour  qui tend vers
qui tend vers
 ? Converge-t-elle ? Diverge-t-elle ? Expliquer.
? Converge-t-elle ? Diverge-t-elle ? Expliquer.
Solution. Puisque  , pour des
nombres
, pour des
nombres  de plus en plus grands, les nombres
de plus en plus grands, les nombres  deviennent uniformément et définitivement arbitrairement petits. Puisque
deviennent uniformément et définitivement arbitrairement petits. Puisque
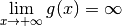 , pour des nombres
, pour des nombres
 de plus en plus grands, les nombres
de plus en plus grands, les nombres 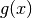 deviennent
uniformément et définitivement arbitrairement grands. Dès lors, pour des
nombres
deviennent
uniformément et définitivement arbitrairement grands. Dès lors, pour des
nombres  de plus en plus petits, les nombres
de plus en plus petits, les nombres  deviennent uniformément et définitivement arbitrairement petits (des
nombres de plus en plus petits auquels on enlève des nombres de plus en
plus grands donnent de plus en plus petits).
deviennent uniformément et définitivement arbitrairement petits (des
nombres de plus en plus petits auquels on enlève des nombres de plus en
plus grands donnent de plus en plus petits).
Exercice 3.8.28. En utilisant les propriétés des limites et des divergences, déterminer les limites ou les divergences suivantes.