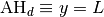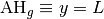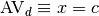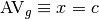3.7 Asymptotes

Il existe une autre manière d’interpréter et de visualiser certaines limites. Ce point de vue plus géométrique des limites que sont les asymptotes plaît énormément à certains mais n’apporte rien de fondamental à l’idée de limite. Passons rapidement en revue les deux types les plus simples d’asymptotes : les asymptotes horizontales et les asymptotes verticales.

Une fois de plus, commençons avec un exemple.

Exemple 3.7.1. Voici ci-dessous le graphe de la fonction :

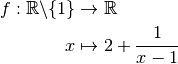
Les limites et les divergences intéressantes pour cette fonction sont :

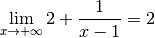
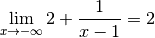
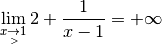
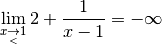
Rappelons-nous ce que signifie en français la première de ces quatre affirmations : au fur et à mesure que devient grand, les nombres 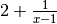associées se rapprochent uniformément et définitivement de 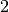. Une autre façon d’exprimer cela, plus géométrique, est de dire que plus on considère des points du graphe de la fonction dont les abscisses sont grandes, plus le graphe de se rapproche uniformément et définitivement de la droite d’équation :

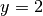Cette droite est ce qu’on appelle une asymptote (horizontale) de la fonction . Son sens est exactement celui encodé par la limite .

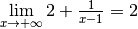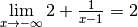Remarquons que la limite peut également être interprétée géométriquement avec une asymptote horizontale : plus on considère des points du graphe de la fonction dont les abscisses sont petites, plus le graphe de se rapproche uniformément et définitivement de la droite d’équation 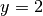également.

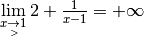Par contre, si on souhaite interpréter les deux affirmations et 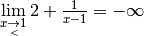de façon plus géométrique, il faut recourir à la notion d’asymptote verticale. Pour cet exemple, on dira que la focntion a une asymptote verticale d’équation cartésienne :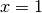

Plus on on considère des points du graphe de dont les abscisses sont proches de , plus le graphe de se rapproche uniformément et définitivement de cette droite. Le sens de cette asymptote verticale est exactement celui des deux divergences 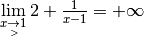et .

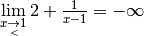Les asymptotes horizontales sont donc juste une manière plus géométrique d’exprimer des limites pour qui tend vers ou de fonctions et les asymptotes verticales sont juste une manière plus géométrique d’exprimer des divergences en un point de fonctions. Donnons les définitions précises de ces deux nouvelles notions.

Définition 3.7.2. Soit un intervalle 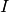non majoré. Soit .

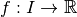Si , on dit que a une asymptote horizontale (à droite) d’équation cartésienne et on note :

Définition 3.7.3. Soit un intervalle 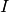non minoré. Soit .

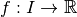Si , on dit que a une asymptote horizontale (à gauche) d’équation cartésienne et on note :

Définition 3.7.4. Soit un intervalle 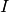éventuellement privé d’un point . Soit .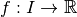

Si ou , on dit que a une asymptote verticale (à droite) d’équation cartésienne et on note :

Définition 3.7.5. Soit un intervalle 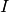éventuellement privé d’un point . Soit .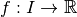

Si ou , on dit que a une asymptote verticale (à gauche) d’équation cartésienne et on note :

Remarque 3.7.6. Il existe encore au moins un autre type d’asymptote : les asymptotes obliques. Nous n’en parlerons pas dans ce cours.

Puisque les asymptotes ne sont qu’une réinterprétation géométrique de certaines limites, il n’y a pas grand chose d’autre à dire à leur sujet. Passons donc immédiatement aux exercices.

Exercice 3.7.7. Pour les fonctions dont les graphes sont donnés ci-dessous, lister toutes les asymptotes horizontales et verticales et donner leurs équations cartésiennes.

Exercice 3.7.8. Donner le graphe d’une fonction qui possède deux asymptotes horizontales (différentes), deux asymptotes verticales dont une des deux a pour équation cartésienn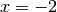e . Donner les équations cartésiennes de toutes les asympotes horizontales et verticales de la fonction choisie.

Solution.

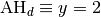
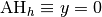
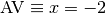
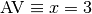
Exercice 3.7.9. Pour les fonctions suivantes, déterminer les équations cartésiennes de toutes les asymptotes horizontales et verticales.