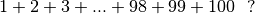1. Introduction¶

Combien fait :

Selon la légende, Johann Carl Friedrich Gauss, un des plus grands mathématiciens de l’histoire, aurait donné la réponse à cette question après seulement 10 secondes alors qu’il avait 10 ans. À son époque, les calculatrices n’existaient même pas : comment est-il parvenu à réaliser cet exploit ? A-t-il véritablement calculé mentalement cette longue somme en moins de 10 secondes ?

Contrairement à ce que de nombreuses personnes pensent, les
mathématiques et le calcul sont deux choses bien différentes. En fait,
un des buts des mathématiciens est souvent de réfléchir à la meilleur
manière d’aborder un problème de telle sorte à avoir à réaliser le
moins de calculs possibles. Si la légende est vraie, Gauss n’a
certainement pas effectué mentalement cette somme en moins de 10
secondes : il a très probablement utilisé ce que nous désignons
aujourd’hui comme la méthode (et la formule) pour calculer la somme
d’un nombre choisi de termes consécutifs d’une suite arithmétique,
méthode que nous allons découvrir dans ce chapitre.

Ce chapitre est dédié aux suites, un outil simple qui permet de
s’entraîner à la manipulation d’outils formels, de formaliser certains
problèmes de façon efficace ou encore de comprendre la différence
entre intérêts simples et intérêts composés. Dans ce cours, ce
chapitre qui est de loin le plus facile de l’année sert également à
donner le temps nécessaire à ceux qui en ont besoin pour se remettre à
niveau.

Pour cette raison, les difficultés de ce chapitre ont été écartés 1
et les prérequis ont été réduit au maximum. Il reste néanmoins
souhaitable :

D’être à l’aise avec le formalisme de base des fonctions.
D’être capable de résoudre des problèmes (dont la difficulté correspond aux problèmes étudiés en quatrième année).

Le chapitre de rappels et compléments est là pour vous aider à combler
d’éventuels lacunes. N’hésitez pas à aller jeter (à nouveau) un œil
sur la partie consécrée aux fonctions un peu plus tôt que prévu si
vous percevez que cela est nécessaire.

Il est à noter que ce chapitre est volontairement incomplet dans le
sens où une partie de la matière a été indiquée comme optionnelle. En
effet, cette partie optionnelle correspond principalement à une
manière spécifique d’introduire la complexe notion de limite. Nous
avons choisi d’introduire celle-ci d’une autre façon, que nous
découvrirons dans le chapitre suivant. Néanmoins, cette partie
optionnelle est très intéressante en soi et peut (grandement) aider à
comprendre la notion de limite par après. Pour cette raison, je vous
invite vivement à la lire durant les vacances de Toussaint.

1: Nous les retrouverons avec un autre point de vue dans le prochain chapitre.