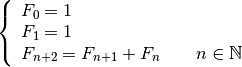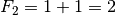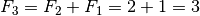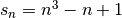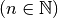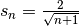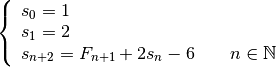2 Suites

Dans cette section, nous allons introduire la notion de suite. Une suite (de nombres) n’est rien d’autre qu’une succession infinie indexée (par les nombres naturels) de nombres.

2.1 Définitions

Définition 2.1.1. Une suite est une fonction de 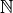dans : .

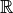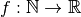Exemple 2.1.2. Les fonctions suivantes :

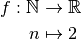
et

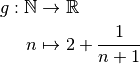
sont deux suites dont les termes sont et 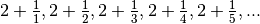. On ne peut évidemment pas donner tous les termes de ces deux suites : il y en a une infinité.

Contre-exemple 2.1.3. La fonction

n’est pas une suite.

Notation. Les lettres 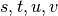sont souvent utilisées pour les suites. Plutôt que d’écrire 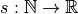pour déclarer une suite, on écrit souvent 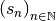. Plutôt que d’écrire 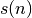, ce qui est souvent nommé terme de rang de la suite , on écrit souvent . Dans ce document, nous reprendrons ces conventions communément admises.

Remarque 2.1.4. Comme pour les fonctions, il est possible de représenter les suites dans un graphe orthonormé. Par exemple, la suite

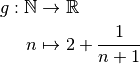
a le graphe suivant :

Attention à ne pas relier les points du graphe ! Dans le cas des suites, le domaine de définition est 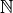, pas !

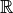Il y a deux manières de définir une suite particulière. On peut la définir comme une fonction : c’est ce qui a été fait à l’exemple 2.1.2. Dans ce cas, on dit qu’on donne la suite en fonction du rang puisqu’on possède alors une formule qui nous permet de calculer directement le terme de rang de la suite ( étant un nombre naturel choisi).

Mais il existe une autre manière de déclarer une suite, dite par récurrence. Celle-ci consiste à donner le ou les premiers termes de la suite, puis donner une règle générale permettant de calculer tous les termes suivants à partir de ce ou ces premiers termes. Plutôt que de donner la définition générale et abstraite de suite définie par récurrence (qui est assez technique), donnons un exemple très connu de suite définie par récurrence : la suite de Fibonacci.

Exemple 2.1.5.

La suite de Fibonacci est l’unique suite telle que :

Autrement dit, on donne les deux premiers termes de la suite, et , et la règle générale nous dit ici que pour obtenir un terme de la suite, il suffit d’additionner les deux précédents. Par exemple, que vaut le terme de rang de la suite, c’est-à-dire ? En prenant dans la formule générale, on sait qu’on doit avoir pour la suite :

Autrement dit :

Donc :

Puisqu’on connait , on peut alors particulariser la formule générale non plus en mais en pour découvrir comment calculer à partir de et :

Et ainsi de suite. On peut calculer que les premiers termes de la suite de Fibonacci sont .

La suite de Fibonacci est fascinante et très populaire car elle apparaît spontanément dans la nature, que ce soit dans les fleurs de tournesol ou dans les coquilles de certains mollusques. De plus, elle est reliée à un nombre qui a eu autrefois énormément d’importance en architecture et en art : le nombre d’or. Malheureusement, nous n’avons pas la possibilité dans ce cours de nous étendre sur le sujet.

L’exemple de la suite de Fibonacci comprend toute la généralité nécessaire pour manipuler les suites définies par récurrence que nous rencontrerons. La plupart du temps, seul le premier terme de la suite est donné et la règle générale de récurrence ne dépent seulement que d’un seul terme (contrairement au cas de la suite de Fibonacci, où elle dépend de deux termes ( et )).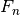

Remarque 2.1.6. Une suite définie en fonction du rang est souvent plus facile à manipuler qu’une suite donnée par récurrence, mais il est parfois plus facile de définir une suite par récurrence.

Dans les deux sections suivantes, nous allons étudier deux types de suites pour lesquels il est aisé de passer de la formulation en fonction du rang à la formulation par récurrence et vice-versa.

Exemple 2.1.7. Soit 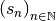une suite telle que :

1.       

2.       

3. 

4. 

5.       

Pour chacune de ces possibilités :

• Calculer 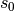, 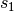et le terme de rang .

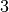• Représenter graphiquement les premiers termes de la suite.