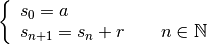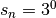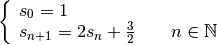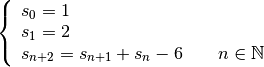2.2 Suites arithmétiques¶
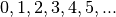
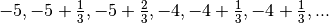
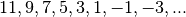
 , pour la deuxième, ce nombre est
, pour la deuxième, ce nombre est  , pour
la troisième, ce nombre est
, pour
la troisième, ce nombre est 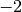 . C’est le principe qui définit
les suites arithmétiques.
. C’est le principe qui définit
les suites arithmétiques.Définition 2.2.1.
Une suite arithmétique est une suite
telle que :
où
est le terme initial et
est la raison (ce qu’on ajoute pour passer d’un terme au suivant).
Exemple 2.2.2. La suite dont les premiers termes sont 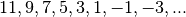 est une suite arithmétique de terme initial
est une suite arithmétique de terme initial 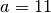 et de raison
et de raison
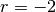 .
.
Remarque 2.2.3. Puisque pour passer d’un terme au suivant dans une suite arithmétique,
il suffit d’ajouter la raison, les termes successifs d’une suite
arithmétique de terme initial 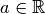 et de raison
et de raison
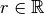 peuvent être notés :
peuvent être notés :
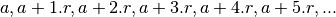
Il n’est dès lors pas surprenant qu’on puisse démontrer qu’une suite
arithmétique de terme initial 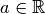 et de raison
et de raison
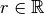 est égale à la suite :
est égale à la suite :
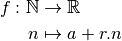
Ce qui correspond à la définition de cette suite en fonction du rang.
Exemple 2.2.4. La suite dont les premiers termes sont 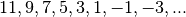 est une suite arithmétique de terme initial
est une suite arithmétique de terme initial 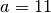 et de raison
et de raison
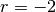 . Elle est égale à la suite :
. Elle est égale à la suite :
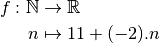
Et en effet, on calcule : 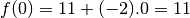 ,
,
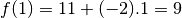 ,
, 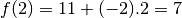 ,
,
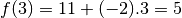 , …
, …
Exercice 2.2.5. Soit 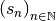 une suite arithmétique telle que
:
une suite arithmétique telle que
:
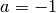 et
et 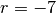
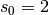 et
et 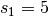
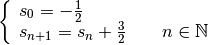
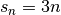
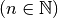
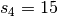 et
et 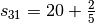
Pour chacune de ces possibilités, calculer  ,
,  et le
terme de rang
et le
terme de rang 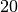 .
.





Exercice 2.2.6. Soit 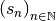 une suite telle que :
une suite telle que :
Pour chacune de ces possibilités, déterminer s’il s’agit d’une suite arithmétique.




Exercice 2.2.7.