2 Fonctions continues¶
2.1 Définition et exemples¶
Définition 2.1.1. Soit 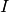 un intervalle éventuellement privé d’un point. Soit
un intervalle éventuellement privé d’un point. Soit
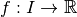 .
.
On dit que
est une fonction continue en
si et seulement si pour tout
, il existe
tel que pour tout
tel que
, on a
.
Remarque 2.1.2. Cette définition, assez technique, ne doit pas vous faire peur. Une
lecture intuitive de cette définition est la suivante : si un
processus  qui dépend d’une variable
qui dépend d’une variable  est continu
autour d’une certaine valeur de
est continu
autour d’une certaine valeur de  qui vaut
qui vaut  , alors je
dois pouvoir approcher les valeurs de
, alors je
dois pouvoir approcher les valeurs de 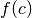 autant que je le
souhaite si je suis capable d’approcher la valeur de
autant que je le
souhaite si je suis capable d’approcher la valeur de  autant
que nécessaire.
Il est recommandé d’appliquer cette définition sur les deux exemples
suivants afin d’analyser celle-ci en profondeur et comprendre en quoi
elle formalise l’idée intutive de continuité.
autant
que nécessaire.
Il est recommandé d’appliquer cette définition sur les deux exemples
suivants afin d’analyser celle-ci en profondeur et comprendre en quoi
elle formalise l’idée intutive de continuité.
Exemple 2.1.3.
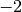 définie sur
définie sur
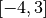 . En effet, quelle que soit l’erreur maximale autorisée
. En effet, quelle que soit l’erreur maximale autorisée
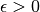 , quitte à sélectionner des valeurs pour
, quitte à sélectionner des valeurs pour  assez proche de
assez proche de 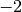 (à une distance de
(à une distance de 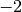 d’au plus
d’au plus
 ), les valeurs
), les valeurs  approcheront bien la
valeur
approcheront bien la
valeur 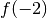 avec une erreur plus petite ou égale à
avec une erreur plus petite ou égale à
 .
.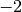 et que le graphe peut être réalisé d’un seul
trait.
et que le graphe peut être réalisé d’un seul
trait.Exemple 2.1.4.
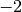 définie sur
définie sur
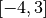 . En effet, en prenant comme erreur maximale autorisée
. En effet, en prenant comme erreur maximale autorisée
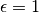 , il est impossible de trouver un
, il est impossible de trouver un  tel qu’à toutes les valeurs de
tel qu’à toutes les valeurs de  possibles à une distance au
plus
possibles à une distance au
plus 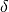 de
de 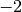 , la fonction
, la fonction  associera un
nombre
associera un
nombre  dont la distance avec
dont la distance avec 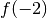 est plus
petite que
est plus
petite que  . La raison étant que juste à gauche de
. La raison étant que juste à gauche de 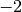 , la fonction prend des valeurs strictement négative alors que
, la fonction prend des valeurs strictement négative alors que
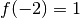 .
.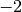 et que le graphe ne peut pas être réalisé d’un seul trait.
et que le graphe ne peut pas être réalisé d’un seul trait.Remarque 2.1.5. Une caractérisation intuitive des graphes de fonctions continues est qu’il s’agit des fonctions dont le graphe peut être tracé d’un seul trait. Néanmoins, celle-ci est imprécise et peut mener à des erreurs, puisque la continuité ne concerne que les sauts dans les valeurs d’une fonction (autrement dit : les sauts verticaux dans le graphe de la fonction) et non son domaine de définition (les sauts horizontaux dans le graphe de la fonction). Permettons-nous d’insister : il ne fait pas sens de parler de continuité d’une fonction en un point où elle n’est pas définie ! Par exemple, la fonction inverse :
Cette fonction est bien partout continue ! Il ne fait pas sens
d’affirmer qu’elle est discontinue en  , puisqu’elle n’est même
pas définie en
, puisqu’elle n’est même
pas définie en  .
.
Définition 2.1.6. Soit 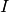 un intervalle éventuellement privé d’un point. Soit
un intervalle éventuellement privé d’un point. Soit 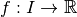 .
.
On dit que
est une fonction continue si elle est continue en tous les points de son domaine de définition.
Exercice 2.1.7. Donner le domaine de définition des fonctions dont les graphes sont les suivants, puis déterminer si elles sont continues ou non. Si elles ne sont pas continues, donner l’ensemble des points où elles sont discontinues.









