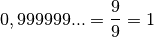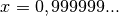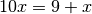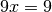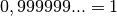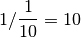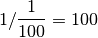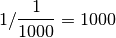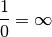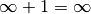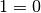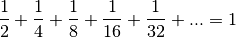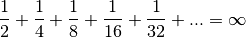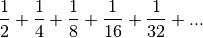3 Introduction aux limites de suites (optionnel)¶
L’infini est une notion qui a intéressé et effrayé les hommes depuis au moins la Grèce Antique. Manipulée de façon intuitive, cette notion est difficile à cerner et peut mener à ce qu’on appelle des paradoxes, des affirmations qui semblent défier la logique car ne pouvant être ni vraies, ni fausses. C’est seulement au dix-neuvième siècle, grâce au travail de Karl Weierstrass, que les mathématiciens sont parvenus à formaliser correctement cette idée étrange qu’est l’infini. Cette découverte est d’autant plus incroyable qu’elle a mené à la naissance de l’analyse mathématique moderne, la branche des mathématiques qui étudie les nombres (réels) et ce qu’il est possible de faire à l’aide de ceux-ci.
Il est à noter que le travail de Georg Cantor, quelques années plus tard, a permis d’étudier mathématiquement l’infini d’une autre manière que ce que permet l’analyse. Néanmoins, nous ne pourrons malheureusement pas aborder cet autre point de vue dans ce chapitre. Pour commencer notre voyage vers la compréhension de l’infini, intéressons-nous à quelques situations simples où l’infini semble jouer un rôle et où un point de vue purement naïf et intuitif de cette notion nous mène à de mystérieuses considérations.
3.1 0,999999… = 1 ?¶
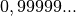 (avec une
infinité de chiffres
(avec une
infinité de chiffres  derrière la virgule) et
derrière la virgule) et  . Si
le premier peut sembler plus petit que le second, les règles de
transformation des nombres à virgules en fraction laisse à penser que
non :
. Si
le premier peut sembler plus petit que le second, les règles de
transformation des nombres à virgules en fraction laisse à penser que
non :
Bien entendu, à ce stade, ces règles peuvent sembler complétement arbitraires. Néanmoins, remarquons qu’un peu de calcul algébrique audacieux nous fait arriver à la même conclusion :
Mais le passage de la première ligne à la deuxième pose question : s’il y a une infinité de chiffres
derrière la virgule, peut-on vraiment dire que
?
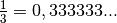 ), il est inquiétant de constater que
le sens de cette notation n’est pas sans équivoque. Cette notation est
d’autant plus problématique qu’elle ouvre la porte à d’autres
questions difficiles faisant intervenir l’infini, telles que
), il est inquiétant de constater que
le sens de cette notation n’est pas sans équivoque. Cette notation est
d’autant plus problématique qu’elle ouvre la porte à d’autres
questions difficiles faisant intervenir l’infini, telles que
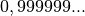 est-il infiniment proche de
est-il infiniment proche de  , sans être
égal à
, sans être
égal à  ? ou si
? ou si 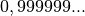 est un nombre, qu’en
est-il de
est un nombre, qu’en
est-il de 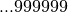 ? .
? .3.2 La division par 0¶
 est parfois présentée comme
une règle d’or des mathématiques. Mais finalement, pourquoi ne peut-on
pas diviser par
est parfois présentée comme
une règle d’or des mathématiques. Mais finalement, pourquoi ne peut-on
pas diviser par  ? Essayons de braver cet interdit.
? Essayons de braver cet interdit.
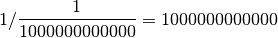

 par
par  , il semble a priori raisonnable d’affirmer que
le résultat de cette division doit être un nombre plus grand que tous
les autres :
, il semble a priori raisonnable d’affirmer que
le résultat de cette division doit être un nombre plus grand que tous
les autres : 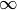 .
.
Cette idée pose cependant vite question. En effet, si
est un nombre plus grand que tous les nombres, on devrait avoir :
Mais alors, en soustrayant
des deux côtés de l’équation :
Ce qui est assez problématique.
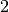 par
par  donne
donne 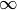 . Mais si
. Mais si
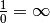 et
et 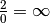 , on
devrait avoir
, on
devrait avoir 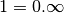 et
et 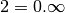 et donc
et donc
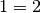 . En fait, si on considère intuitivement que le résultat de
n’importe quel nombre strictement positif par
. En fait, si on considère intuitivement que le résultat de
n’importe quel nombre strictement positif par  doit donner
doit donner
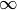 , on peut montrer ainsi que
, on peut montrer ainsi que  est égal à
n’importe quel nombre strictement positif !
est égal à
n’importe quel nombre strictement positif !3.3 Le paradoxe de la flèche¶
Ce paradoxe date d’il y a plus de  ans et est généralement
associé à Zénon, un Grec de la Grèce antique qui collectionnait les
paradoxes. Le paradoxe est connu comme le paradoxe de la flèche (ou le
paradoxe de l’archer) et a une variante faisant intervenir une tortue
et Achille (ou un lièvre). Nous allons donner ici la première version.
Imaginons un archer situé à une distance de
ans et est généralement
associé à Zénon, un Grec de la Grèce antique qui collectionnait les
paradoxes. Le paradoxe est connu comme le paradoxe de la flèche (ou le
paradoxe de l’archer) et a une variante faisant intervenir une tortue
et Achille (ou un lièvre). Nous allons donner ici la première version.
Imaginons un archer situé à une distance de  dam de sa
cible. Lorsque l’archer va décocher une flèche, celle-ci va parcourir
la distance qui la sépare de la cible, jusqu’au moment où elle la
touchera, ce qui arrive en un temps fini.
dam de sa
cible. Lorsque l’archer va décocher une flèche, celle-ci va parcourir
la distance qui la sépare de la cible, jusqu’au moment où elle la
touchera, ce qui arrive en un temps fini.
Néanmoins, Zénon fait remarquer que la flèche, avant d’atteindre la
cible, devra d’abord parcourir la moitié de la distance qui la sépare
de la cible. De plus, une fois que la flèche aura parcouru cette
première moitié de la distance qui la sépare de la cible (une distance
de  dam), la flèche devra d’abord parcourir la
moitié de la distance restante (c’est-à-dire
dam), la flèche devra d’abord parcourir la
moitié de la distance restante (c’est-à-dire
 dam). Ensuite, à nouveau, la flèche devra d’abord
parcourir la moitié de la distance restante (c’est-à-dire
dam). Ensuite, à nouveau, la flèche devra d’abord
parcourir la moitié de la distance restante (c’est-à-dire
 dam). Et ainsi de suite sans qu’il arrive un
moment où la distance qui sépare la flèche de la cible soit nulle !
Puisque la flèche devrait parcourir une infinité de distances, Zénon
en conclut qu’il lui faudrait un temps infini pour arriver à la cible.
Néanmoins, Zénon est bien conscient que s’il réalise l’expérience…
la flèche touchera la cible. C’est un paradoxe.
dam). Et ainsi de suite sans qu’il arrive un
moment où la distance qui sépare la flèche de la cible soit nulle !
Puisque la flèche devrait parcourir une infinité de distances, Zénon
en conclut qu’il lui faudrait un temps infini pour arriver à la cible.
Néanmoins, Zénon est bien conscient que s’il réalise l’expérience…
la flèche touchera la cible. C’est un paradoxe.
Si on souhaite formuler un peu plus mathématiquement le paradoxe, on peut le faire comme suit. L’intuition physique nous dit que :
Tandis que l’argument de Zénon consiste à dire que :
Nous verrons plus tard que la notion de limite permet de choisir l’égalité la plus pertinente et de comprendre d’où provient la confusion.
3.4 Des sommes infinies¶
A priori, il n’est pas clair qu’on puisse attribuer à cette suite de symboles un sens quelconque. Après tout, les êtres humains que nous sommes ne peuvent jamais qu’additionner un nombre fini de termes puisqu’il semble que notre vie est finie.
- Il ne fait pas sens de considérer
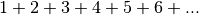 comme un
nombre réel.
comme un
nombre réel. - Il fait sens de considérer
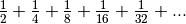 comme un nombre réel et on a l’égalité
comme un nombre réel et on a l’égalité
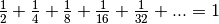 .
. - Il ne fait pas sens de considérer
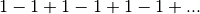 comme un
nombre réel (on ne dira donc pas que cette somme infinie est égale
à
comme un
nombre réel (on ne dira donc pas que cette somme infinie est égale
à 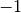 ,
,  ou
ou  ).
). Il ne fait pas sens de considérer
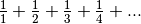 comme un
nombre réel… mais il fait sens de considérer
comme un
nombre réel… mais il fait sens de considérer
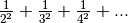 comme un nombre
réel et on a l’égalité
comme un nombre
réel et on a l’égalité
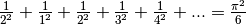 .
.