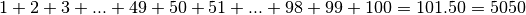2.5 Sommes de suites¶
Dans cette section, nous allons découvrir les méthodes et formules pour
la somme des 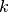 premiers termes d’une suite arithmétique ou
géométrique donnée, où
premiers termes d’une suite arithmétique ou
géométrique donnée, où 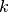 est un nombre naturel choisi. Mais
commençons par l’exemple de l’introduction :
est un nombre naturel choisi. Mais
commençons par l’exemple de l’introduction :
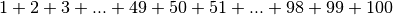 ?
? avec
avec
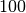 ,
, 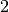 avec
avec 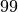 ,
, 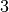 avec
avec 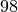 , …
,
, …
, 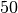 avec
avec 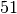 . Toutes ces paires donnent
. Toutes ces paires donnent 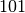 et
il y a
et
il y a 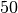 paires. On en déduit que :
paires. On en déduit que :
Cette simple idée va nous permettre de démontrer la formule pour la somme des
(
) premiers termes d’une suite arithmétique.
Proposition 2.5.2. Soit 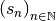 une suite
arithmétique de terme initial
une suite
arithmétique de terme initial 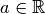 et de raison
et de raison
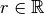 . Choisissons un nombre
. Choisissons un nombre
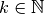 . Notons la somme des termes de la suite
. Notons la somme des termes de la suite
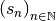 pour les rangs de
pour les rangs de  à
à
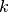 de la façon suivante :
de la façon suivante :
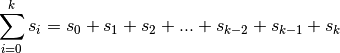
Alors on a :
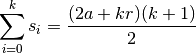
Démonstration Puisque 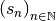 une suite arithmétique de
terme initial
une suite arithmétique de
terme initial 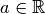 et de raison
et de raison
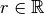 , on a pour
, on a pour 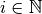 :
:
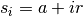 . Dès lors :
. Dès lors :
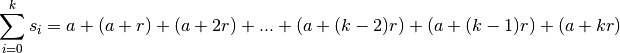
On peut écrire cette somme dans l’autre sens :

Additionnons les deux égalités précédentes et groupons ensemble le premier terme de la somme du membre de droite de la première égalité avec le premier terme de la somme du membre de droite de la deuxième égalité, le deuxième terme de la somme du membre de droite de la première égalité avec le deuxième terme de la somme du membre de droite de la deuxième égalité, le troisième terme de la somme du membre de droite de la première égalité avec le troisième terme de la somme du membre de droite de la deuxième égalité et ainsi de suite :
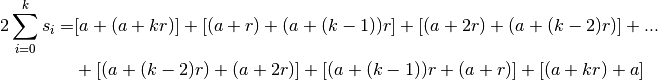
On observe que tous ces rassemblements donnent le même résultat :
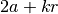 . Ces rassemblements sont au nombre de
. Ces rassemblements sont au nombre de 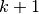 , on a
donc :
, on a
donc :
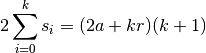
Conclusion :

Nous avons une proposition similaire pour les suites géométriques :
Proposition 2.5.3. Soit 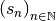 une suite géométrique
de terme initial
une suite géométrique
de terme initial  et de raison
et de raison
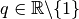 . Choisissons un nombre
. Choisissons un nombre
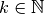 . On a :
. On a :
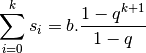
Démonstration Puisque 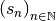 une suite géométrique de
terme initial
une suite géométrique de
terme initial  et de raison
et de raison
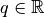 , on a pour
, on a pour 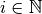 :
:
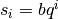 . Dès lors :
. Dès lors :
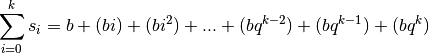
On peut multiplier cette égalité par 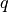 :
:
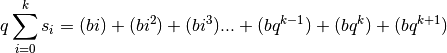
Soustrayons la deuxième égalité à la première en groupant ensemble le deuxième terme de la somme du membre de droite de la première égalité avec le premier terme de la somme du membre de droite de la deuxième égalité, le troisième terme de la somme du membre de droite de la première égalité avec le deuxième terme de la somme du membre de droite de la deuxième égalité, le quatrième terme de la somme du membre de droite de la première égalité avec le troisième terme de la somme du membre de droite de la deuxième égalité et ainsi de suite :

On observe que tous ces rassemblements donnent le même résultat :
 . On a donc :
. On a donc :
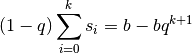
Puisque 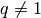 , on conclut :
, on conclut :
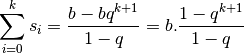
Remarque 2.5.4. Si on souhaite calculer la somme des termes d’une suite arithmétique ou
géométrique non pas à partir de  mais à partir d’un autre
nombre naturel choisi, disons
mais à partir d’un autre
nombre naturel choisi, disons 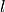 , il est possible de s’en sortir
facilement grâce aux formules des propositions
[sommeari] et [sommegéo] puisque pour
une suite
, il est possible de s’en sortir
facilement grâce aux formules des propositions
[sommeari] et [sommegéo] puisque pour
une suite 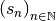 , on a :
, on a :
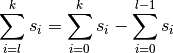
Exercice 2.5.5.


Exercice 2.5.6.




Exercice 2.5.7.


Exercice 2.5.8.