2.4 Intérêts simples et intérêts composés¶
Problème Considérons le problème suivant : nous disposons de 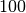 € et
nous avons la possibilité de déposer ces
€ et
nous avons la possibilité de déposer ces 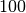 € sur un compte
d’une première banque qui nous propose des intérêts mensuels de
€ sur un compte
d’une première banque qui nous propose des intérêts mensuels de
 % de la somme initiale déposée sur le compte (c’est-à-dire,
dans notre cas,
% de la somme initiale déposée sur le compte (c’est-à-dire,
dans notre cas, 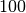 €) ou sur un compte d’une seconde banque
qui elle nous propose des intérêts mensuels de
€) ou sur un compte d’une seconde banque
qui elle nous propose des intérêts mensuels de 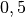 % de la
somme présente sur le compte ce mois-là, somme qui évolue donc chaque
mois. En supposant que nous allons laisser l’argent sur le compte
pendant
% de la
somme présente sur le compte ce mois-là, somme qui évolue donc chaque
mois. En supposant que nous allons laisser l’argent sur le compte
pendant 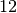 mois, sans y toucher ni y ajouter quelque chose,
quelle est la banque la plus avantageuse (pour nous) ?
mois, sans y toucher ni y ajouter quelque chose,
quelle est la banque la plus avantageuse (pour nous) ?
Commençons par donner la suite des sommes d’argent dont nous
disposerons après les premiers mois si nous choisissons la première
banque : après  mois, nous disposerons de
mois, nous disposerons de
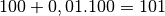 €. Après
€. Après 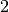 mois, nous
disposerons de
mois, nous
disposerons de 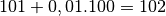 €. Et ainsi de suite :
on remarque qu’on a affaire à une suite arithmétique de terme initial
€. Et ainsi de suite :
on remarque qu’on a affaire à une suite arithmétique de terme initial
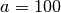 et de raison
et de raison  . Après
. Après 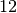 mois, nous
disposerons donc de
mois, nous
disposerons donc de 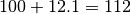 €.
€.
Passons au cas de la deuxième banque. Après le premier mois, nous
disposerons de
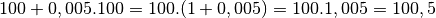 €.
Après le deuxième mois, nous disposerons de
€.
Après le deuxième mois, nous disposerons de
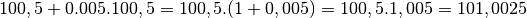 €.
Et ainsi de suite : on remarque qu’on a affaire à une suite
géométrique de terme initial
€.
Et ainsi de suite : on remarque qu’on a affaire à une suite
géométrique de terme initial 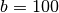 et de raison
et de raison  .
Après
.
Après 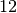 mois, nous disposerons donc de
mois, nous disposerons donc de
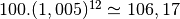 €.
€.
Conclusion : la première banque est la plus intéressante. Néanmoins, ce ne sera pas éternellement le cas : puisque les intérêts de la seconde banque grandissent sans cesse et de plus en plus vite, il est clair que sur le plus long terme (pouvez-vous déterminer à partir de combien de mois ?), la seconde banque est plus intéressante.
Les intérêts que propose la première banque sont ce qu’on appelle des intérêts simples, tandis que ceux que propose la seconde banque sont ce qu’on appelle des intérêts composés. Il est important de se souvenir que les intérêts simples correspondent à une suite arithmétique, tandis que les intérêts composés correspondent à une suite géométrique.
Exercice 2.4.1.
