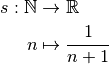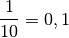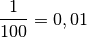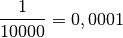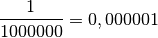4 Limites de suites (optionnel)¶
4.1 Définition¶
Dans l’introduction, nous avons discuté des problèmes qui surgissent
rapidement si l’on considère l’infini comme un nombre réel tel que
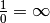 ou encore
ou encore 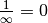 .
.
Néanmoins, si l’on considère par exemple la suite
on aimerait malgré tout pouvoir exprimer clairement l’idée que les termes de cette suite se rapprochent de
, de façon définitive, au fur et à mesure que le rang grandit :
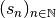 définie ci-dessus se rapproche de
définie ci-dessus se rapproche de
 , de façon définitive, au fur et à mesure que le rang
grandit, il est nécessaire que que pour toute borne réelle strcitement
positive
, de façon définitive, au fur et à mesure que le rang
grandit, il est nécessaire que que pour toute borne réelle strcitement
positive  que l’on se fixe, il doit avoir un certain
que l’on se fixe, il doit avoir un certain
 tel qu’à partir de ce moment
tel qu’à partir de ce moment 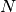 , tous
les termes de la suite sont à une distance au plus
, tous
les termes de la suite sont à une distance au plus  de
de
 (sinon, il existera toujours des termes de la suite qui
s’éloigneront de
(sinon, il existera toujours des termes de la suite qui
s’éloigneront de  plutôt que de s’en rapprocher, quel que
soit l’endroit où on est arrivé dans la suite).
plutôt que de s’en rapprocher, quel que
soit l’endroit où on est arrivé dans la suite).Définition 4.1.1. Soit une suite 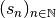 . La suite
. La suite
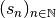 a une limite
a une limite 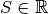 si pour tout nombre réel strictement positif
si pour tout nombre réel strictement positif  , il existe
, il existe
 tel que pour tout
tel que pour tout 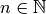 avec
avec
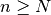 , on a
, on a

Dans ce cas, on note 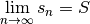 et on
dit que la suite converge vers
et on
dit que la suite converge vers 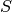 .
.
Passons en revue les suites issues des fonctions de référence et déterminons si elles ont une limite.
Suite obtenue à partir de la fonction constante de constante
 (
( est un nombre réel quelconque) :
est un nombre réel quelconque) :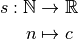
Cette suite a trivialement pour limite
 :
:
 .
.Suite obtenue à partir de la fonction identité :

Cette suite n’a pas de limite.
Suite obtenue à partir de la fonction carrée :
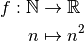
Cette suite n’a pas de limite.
Suite obtenue à partir de la fonction cubique :
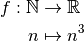
Cette suite n’a pas de limite.
Suite obtenue à partir de la fonction racine carrée :
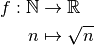
Cette suite n’a pas de limite.
Suite obtenue à partir de la fonction racine cubique :
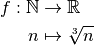
Cette suite n’a pas de limite.
Suite obtenue à partir de la fonction inverse :

Cette suite a comme limite
 :
:
 .
.Suite obtenue à partir de la fonction valeur absolue :

Cette suite n’a pas de limite.
Ces limites de base vont nous permettre de calculer des limites plus complexes grâce aux résultats de la prochaine section.
Exercice 4.1.2 (Difficile). À partir de la définition de limite, démontrer que si
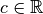 , la suite
, la suite

a pour limite  .
.
Solution Soit un nombre réel strictement positif  fixé. Prenons
fixé. Prenons
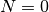 . Alors, pour tout
. Alors, pour tout 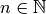 avec
avec
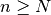 , on a
, on a 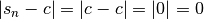 , donc
, donc
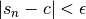 .
.
Exercice 4.1.3 (Très difficile). À partir de la définition démontrer que la suite

a pour limite  .
.
Solution Soit un nombre réel strictement positif  fixé. Prenons
fixé. Prenons
 tel que
tel que 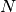 soit strictement plus grand
que
soit strictement plus grand
que  (ce qui implique que
(ce qui implique que
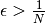 ). Alors, pour tout
). Alors, pour tout
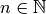 avec
avec 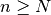 , on a
, on a
 ,
donc
,
donc 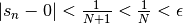 .
.
4.2 Propriétés des limites¶
Donnons à présent plusieurs résultats importants concernant les limites. Commençons par une proposition qui décrit comment se combinent les limites de deux suites convergentes lorsqu’on les combinent entre elles.
Proposition 4.2.1. Soient deux suites 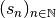 et
et
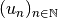 qui convergent respectivement vers
qui convergent respectivement vers
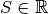 et
et 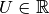 . Alors :
. Alors :
La suite
 converge et on a
converge et on a
 .
.Si
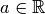 , la suite
, la suite
 converge et on a
converge et on a
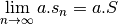 .
.La suite
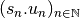 convergent et on a
convergent et on a
 .
.Si
 , la suite
, la suite
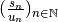 converge et on a
converge et on a
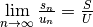 .
.
À présent, décrivons comme intéragissent les limites avec les inégalités (non-strictes) :
Théorème 4.2.2 (Théorème du sandwich). Soient trois suites 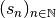 ,
,
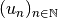 et
et  avec pour tout
avec pour tout 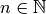 :
: 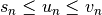 et
telles que
et
telles que 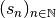 converge vers
converge vers
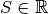 et
et 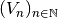 converge
vers
converge
vers 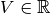 . Alors :
. Alors :
Sa suite
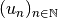 converge vers
converge vers
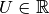 , on a nécessairement
, on a nécessairement  .
.Si
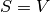 , alors la suite
, alors la suite 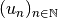 converge nécessairement vers un nombre
converge nécessairement vers un nombre 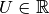 qui
est en fait égal à
qui
est en fait égal à 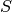 et
et 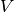 .
.
Pour terminer, donnons un théorème nommé en l’honneur du mathématicien qui a inventé la définition moderne de limite :
Théorème 4.2.3 (Théorème du Weierstrass). Soit une suite 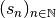 . Si
. Si
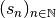 est croissante et est majorée, alors
est croissante et est majorée, alors
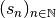 converge nécessairement et sa limite
est le plus petit de ses majorants.
converge nécessairement et sa limite
est le plus petit de ses majorants.
Remarque 4.2.4. Ce théorème reste valable si l’on remplace croissante par décroissante, majorée par minorée et plus petit de ses majorants par plus grand de ses minorants .
Exercice 4.2.5.