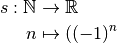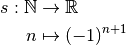4.3 Divergence vers 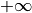 et
et 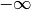 ¶
¶
De la même manière que la notion de limite nous permet d’exprimer
clairement l’idée que la suite qui provient de la fonction inverse se
rapproche de  , de façon définitive, au fur et à mesure que le
rang grandit, la notion de divergence va nous permettre d’exprimer
clairement l’idée que la suite qui provient de la fonction identité (par
exemple) grandit de plus en plus, de façon définitive, au fur et à
mesure que le rang augmente :
, de façon définitive, au fur et à mesure que le
rang grandit, la notion de divergence va nous permettre d’exprimer
clairement l’idée que la suite qui provient de la fonction identité (par
exemple) grandit de plus en plus, de façon définitive, au fur et à
mesure que le rang augmente :
Théorème 4.3.1. Soit une suite 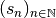 . La suite
. La suite
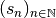 diverge vers
diverge vers 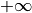 si pour
tout nombre réel
si pour
tout nombre réel 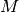 , il existe
, il existe 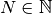 tel que
pour tout
tel que
pour tout 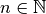 avec
avec 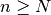 , on a
, on a
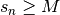
Dans ce cas, on note 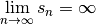 et
on dit que la suite diverge vers
et
on dit que la suite diverge vers 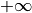 .
.
Remarque 4.3.2. Attention ! Lorsqu’on écrit
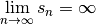 , on ne dit absolument
pas la suite
, on ne dit absolument
pas la suite 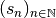 a une limite et que cette
limite est le nombre
a une limite et que cette
limite est le nombre 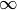 ! La notation est extrêmement
similaire à celle de limite, mais le sens de celle-ci est très
différent.
! La notation est extrêmement
similaire à celle de limite, mais le sens de celle-ci est très
différent.
On peut définir de façon similaire la divergence vers 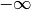 :
:
Définition 4.3.3. Soit une suite 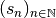 . La suite
. La suite
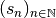 diverge vers
diverge vers 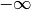 si pour
tout nombre réel
si pour
tout nombre réel 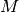 , il existe
, il existe 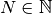 tel que
pour tout
tel que
pour tout 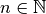 avec
avec 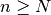 , on a
, on a
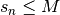
Dans ce cas, on note 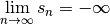 et
on dit que la suite diverge vers
et
on dit que la suite diverge vers 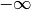 .
.
Passons en revue les suites issues des fonctions de référence et déterminons si elles divergent.
Suite obtenue à partir de la fonction constante de constante
 (
( est un nombre réel quelconque) :
est un nombre réel quelconque) :
Cette suite a pour limite
 et ne diverge pas.
et ne diverge pas.Suite obtenue à partir de la fonction identité :

Cette suite diverge vers
 .
.Suite obtenue à partir de la fonction carrée :
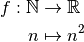
Cette suite diverge vers
 .
.Suite obtenue à partir de la fonction cubique :
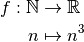
Cette suite diverge vers
 .
.Suite obtenue à partir de la fonction racine carrée :
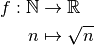
Cette suite diverge vers
 .
.Suite obtenue à partir de la fonction racine cubique :
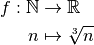
Cette suite diverge vers
 .
.Suite obtenue à partir de la fonction inverse :
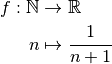
Cette suite a comme limite
 et ne diverge pas.
et ne diverge pas.Suite obtenue à partir de la fonction valeur absolue :

Cette suite diverge vers
 .
.
On a des résultats similaires à ceux de la proposition 4.2.1 pour deux suites divergentes :
Proposition 4.3.4. Soient deux suites 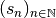 et
et
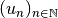 qui divergent toutes les deux vers
qui divergent toutes les deux vers
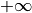 . Alors :
. Alors :
La suite
 diverge vers
diverge vers
 .
.Soit
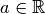 . Si
. Si  , la suite
, la suite
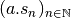 diverge vers
diverge vers  . Si
. Si
 , la suite
, la suite 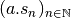 converge
vers
converge
vers  . Si
. Si  , la suite
, la suite
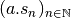 diverge vers
diverge vers  .
.La suite
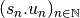 diverge vers
diverge vers
 .
.Pour la division, il n’existe pas de règle générale.
On a également des résultats similaires à ceux de la proposition 4.2.1 pour une suite convergente et une suite divergente :
Proposition 4.3.5. Soient deux suites 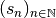 et
et
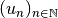 telles que
telles que
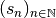 converge vers
converge vers 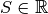 et
et 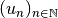 diverge vers
diverge vers  . Alors
:
. Alors
:
La suite
 diverge vers
diverge vers
 .
.Si
 , la suite
, la suite 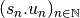 diverge vers
diverge vers  . Si
. Si 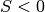 , la suite
, la suite
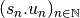 diverge vers
diverge vers  .
Si
.
Si 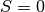 , pas de règle générale.
, pas de règle générale.La suite
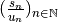 converge vers
converge vers
 .
.Si
 , alors la suite
, alors la suite
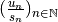 diverge vers
diverge vers
 . Si
. Si 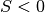 , alors la suite
, alors la suite
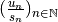 diverge vers
diverge vers
 . Si
. Si 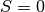 , pas de règle générale.
, pas de règle générale.
Exercice 4.3.6.










Exercice 4.3.7. Un élève a écrit que
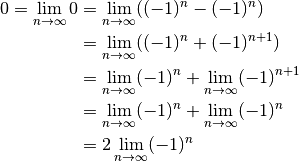
et donc
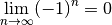
Êtes-vous d’accord avec cette conclusion ? Quelle proposition l’élève a-t-il mal utilisé ? Où se situe son erreur ?
Solution | L’élève a utilisé la proposition [proplim] à l’envers
(ce qui n’est pas correct) : on a bien que
, mais ça n’implique pas que les suites
et
aient une limite et que
.