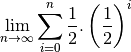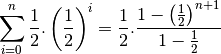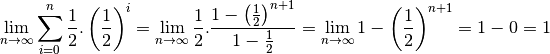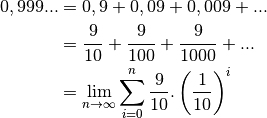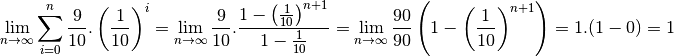5 Conclusion : retour sur les problèmes de l’introduction (optionnel)¶
Finalement, rassemblons tout ce que nous avons appris dans ce chapitre pour résoudre certains des problèmes de l’introduction.
5.1 Paradoxe de la flèche : la solution¶
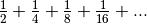 ne peut qu’être infinie car correspondant à une somme d’une infinité
de distances/de termes strictement positifs. Cela contredit
l’intuition géométrique et l’expérience physique, d’où le paradoxe.
ne peut qu’être infinie car correspondant à une somme d’une infinité
de distances/de termes strictement positifs. Cela contredit
l’intuition géométrique et l’expérience physique, d’où le paradoxe.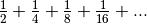 :
on peut en effet la voir comme la limite d’une suite consistant en les
sommes finies des
:
on peut en effet la voir comme la limite d’une suite consistant en les
sommes finies des 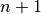 premiers termes d’une suite géométrique
de terme initial
premiers termes d’une suite géométrique
de terme initial 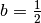 et de raison
et de raison
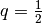 :
:
De plus, nous avons à présent une formule pour calculer ces sommes finies :
Et nous sommes donc en mesure de calculer notre limite :
Contrairement à ce que Zénon pensait, la suite
ne diverge pas vers
mais converge bien vers
! Cela rejoint l’intuition géométrique et l’expérience physique : le paradoxe est donc résolu.
5.2 0,999… < 1 ou 0,999… = 1 ?¶
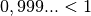 ou
ou 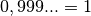 ?
? expriment la présence d’une limite
dissimulée. En fait, lorsqu’on écrit
expriment la présence d’une limite
dissimulée. En fait, lorsqu’on écrit 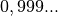 , on écrit de
façon raccourcie la limite suivante :
, on écrit de
façon raccourcie la limite suivante :
(Le fait que les
correspondent à une limite n’est pas révélé en primaire ou en début de secondaire pour des raisons évidentes.)
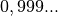 , nous devrions être également capables de démontrer
si ce nombre est strictement plus petit que
, nous devrions être également capables de démontrer
si ce nombre est strictement plus petit que  ou égal à
ou égal à
 :
:
Ce qui clôt la discussion.
Exercice 5.2.1. On vous affirme depuis longtemps que 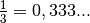 . En
écrivant correctement
. En
écrivant correctement 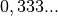 sous la forme d’une limite,
démontrez-le.
sous la forme d’une limite,
démontrez-le.
Solution
|
| 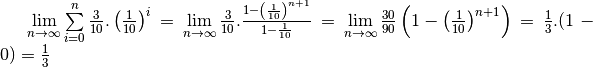
Exercice 5.2.2.

Exercice 5.2.3.

- 1
Nous les retrouverons avec un autre point de vue dans le prochain chapitre.